图论——最小生成树

• Prim（普里姆算法）
• Kruskal（克鲁斯卡尔算法）
• 最小生成树例题

Prim算法

每次找最小值即可

上代码

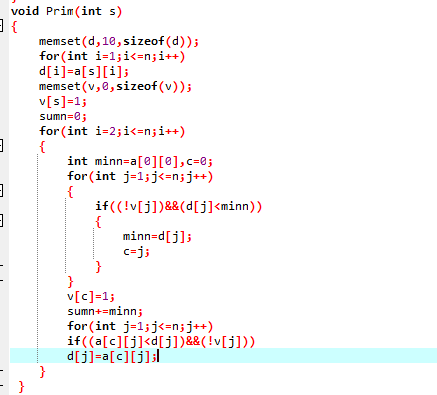
此算法我本人是几乎没有用过，因为Prim+堆优化和Kruskal都对稀疏图比较好，本人比较喜欢Kruskal，所以几乎对这个算法没有什么太多的了解，只是知道大致的原理，就是在一个点上，找一个最小边权的边，然后进行扩展。

Kruskal算法

这个算法本人经常使用，这个算法需要有并查集的基础，排序的基础，算法主要思想就是先给边权从小到大排序，然后再用并查集合并起来。因为是最小生成树，所以不能让它成环，所以在合并的边数等于n-1时，跳出循环。

上代码

一个合并函数

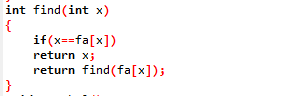
并查集find函数

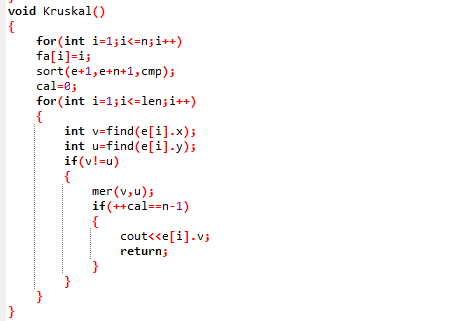
Kruskal主要函数

上面三个函数构成了Kruskal算法。

我认为Kruskal还是比较好用的，也比较好理解，代码也比较简洁，推荐！

最小生成树例题

边权差值最小的生成树

题面描述

样例

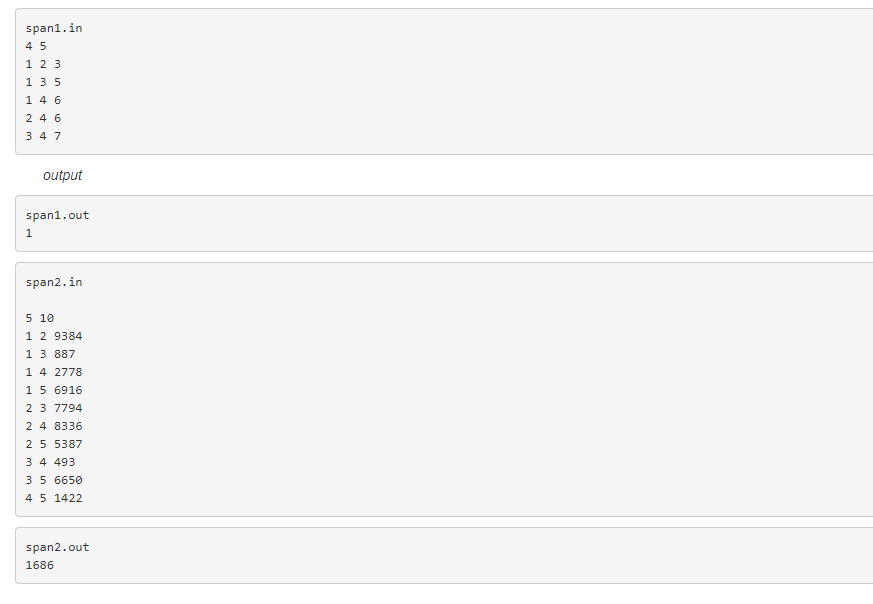
数据范围

题目分析

首先看到题目的最小生成树，所以就直接确定了算法，为Kruskal和Prim算法，在此我还是使用我熟悉的Kruskal，题目要求要找边权差值最小的，所以就很容易能想到，在算法的基础上输出的时候不用输出边权值，而是输出差值，这样就可以了。

#include<bits/stdc++.h>
using namespace std;
struct hf
{
	int x,y;
	int z; 
}e[1000005];
bool cmp(hf o,hf p)
{
	return o.z<p.z;
}
int fa[1000005];
int cnt=0,op1[1000005],op2[1000005],l[5000][5000];
int find(int x)
{
	if(x==fa[x])
	return x;
	return find(fa[x]);
}
int main()
{
	freopen("span.in","r",stdin);
	freopen("span.out","w",stdout);
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>e[i].x>>e[i].y>>e[i].z;
	}
	sort(e+1,e+m+1,cmp);
	int cal=0;
	int sum=0,minn=e[m].z;
//	cout<<cnt<<endl;
	int i; 
	for(int kl=1;kl<=m;kl++)
	{
		cal=0;
		for(i=1;i<=n;i++)
		fa[i]=i;
		for(i=kl;i<=m;i++)
		{
			int v=find(e[i].x);
			int u=find(e[i].y);
			if(v!=u)
			{
				fa[v]=u;
				if(++cal==n-1)
				{
					minn=min(minn,e[i].z-e[kl].z); 
					break;
				}
			 } 
		 } 
	}
	if(minn==e[m].z)
	minn=-1;
	cout<<minn; 
	return 0;
}

最后在判断一下minn是否改变，如果不改变，说明不符合，输出-1；