- 最短路
- Dijkstra
- spfa
- spfa的应用
- 第二/第k短路
- spfa判负环
- A*
- Bellman-ford
- Bellman-ford判负环
- Floyd
- 模板
- 输出路径
Dijkstra算法求单源最短路
这个了解的不是很多,我大多数用的都是spfa,但是小根堆优化的Dijkstra和spfa写法大致相同,但是应该是比spfa稳定。
上代码
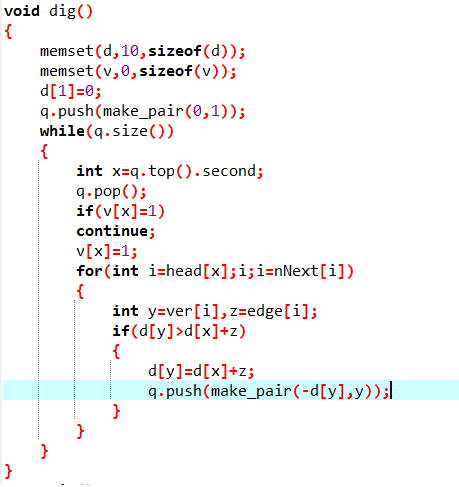
上述代码出自算法竞赛进阶指南,dig模板,o(n^2)的模版在此就不放出了,dig的优点在于稳,速度快,缺点就是不能有负权,有负权时就可以采用速度较快的spfa来解决。因为dig是基于贪心思想的,所以,适用于非负权图。
spfa算法
spfa是我最常用的算法,速度不慢而且能适用于负环图,但是有一个缺点就是他不是很稳,如果是在随机数据下spfa跟dig速度相同,有时还有可能快于dig,但是在特定生成的数据下,spfa就没有dig跑的快了,建议在非负权图上用堆优化的dig。
上代码

上述是spfa的模板,我经常使用的一个模板,邻接表存图,遍历,spfa是由队列实现的,可以用数组模拟队列来实现spfa,我就直接用了queue,毕竟比较懒。
spfa的应用
我一般会用spfa来求第二短路和第k短路,第二短路就是多开一个数组,在最短路更新时更新,最短路不更新是和次短路比较就行了。
上代码
void spfa(int s)
{
memset(d,10,sizeof(d));
memset(d1,10,sizeof(d1));
v[s]=1;
d[s]=0;
queueq;
q.push(s);
while(q.size())
{
int now=q.front();
q.pop();
v[now]=0;
for(int i=head[now];i;i=next2[i])
{
int y=ver[i],z=edge[i];
if(d[y]>d[now]+z)
{
d1[y]=d[y];
d[y]=d[now]+z;
if(!v[y])
{
v[y]=1;
q.push(y);
}
}
else if(d1[y]>d[now]+z&&d[now]+z>d[y])
{
d1[y]=d[now]+z;
if(!v[y])
{
v[y]=1;
q.push(y);
}
}
if(d1[now]+z<d1[y])
{
d1[y]=d1[now]+z;
if(!v[y])
q.push(y),v[y]=1;
}
}
}
}
第k短路的话那就需要一个其他的算法了——A*
启发式搜索,我之前根本就没有了解过,本以为没有什么用,到此时发现了这个神奇的作用。
咱们首先来介绍一下A*算法
A*算法又称估价函数,以任意状态为输入,计算出从该状态到目标状态所需要的估价值。估计值一定要小于等于实际值,如果违背了这个原则会导致答案错误,错过你所要的方案。具体证明可以用反证法来证明。
上代码
void spfa(int s)
{
memset(d,INF,sizeof(d));
v[s]=1;
d[s]=0;
queueq;
q.push(s);
while(q.size())
{
int now=q.front();
q.pop();
v[now]=0;
for(int i=head[now];i;i=next2[i])
{
int y=ver[i],z=edge[i];
if(d[y]>d[now]+z)
{
d[y]=d[now]+z;
if(!v[y])
{
v[y]=1;
q.push(y);
}
}
}
}
}
void A_start(int s,int t)
{
int op=2;
hf temp;
if(s==t)
op++;
if(d[s]==INF)
return ;
temp.to=s;
temp.g=0;
temp.f=temp.g+d[s];
q1.push(temp);
while(q1.size())
{
temp=q1.top();
q1.pop();
if(temp.to==t)
{
cnt++;
ans+=temp.g;
}
for(int i=head1[temp.to];i;i=next1[i])
{
hf tt;
tt.to=ver1[i];
tt.g=temp.g+edge1[i];
tt.f=tt.g+d[ver1[i]];
q1.push(tt);
}
}
return ;
}
上述代码就是spfa加A*求第k短路的代码,一定要仔细理解A*的作用,用BFS也可以写第k短路,但是你会惊奇的发现,TLE虽然时间复杂度和A*是一样的,但是,A*却能过,这可能就是神奇的事情吧。
spfa判负环
一个数进队>=n次时,就说明当中有负权值,因为spfa的松弛方法和Bellman-ford是一样的,所以,其中某一个点被松弛次数>=n时,就说明有负环。
上代码
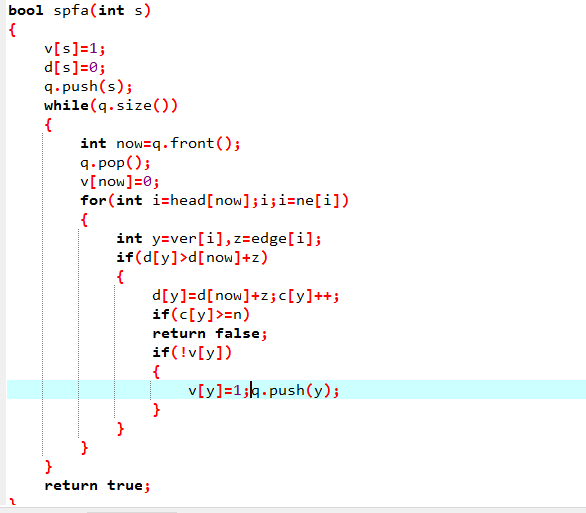
c数组就是用来判断松弛的次数,从而进行判断是否有负环。
Bellman-ford算法
这个算法主要是用于判断负环,几乎不用他来求最短路,判断负环的话Bellman-ford算法比spfa的效率要高。
上代码
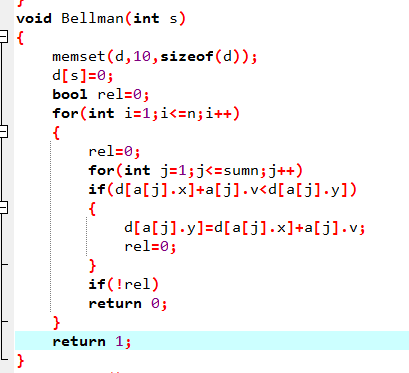
Floyd算法
弗洛伊德算法是最厉害的算法,是应用最广的算法,代码简洁,可以用于负环图,由三重循环构成,Floyd是多源最短路,所以可以,求出任意点到任意点的最短路径,方程为:
d[k,i,j]=min(d[k-1,i,j],d[k-1,i,k]+d[k-1,k,j]);
Floyd的本质是动态规划(DP),在背包问题当中,我们可以知道k循环可以省略,所以就得到了二维方程:
d[i,j]=min(d[i,j],d[i,k]+d[k,j]);
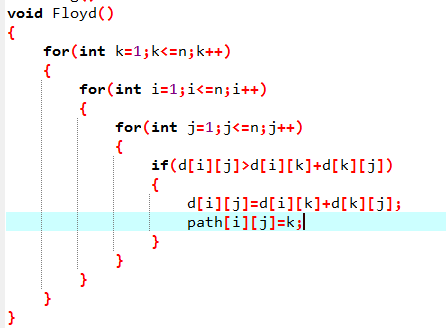
二话不说,上代码

上述就是Floyd的代码模板。
Floyd的应用
输出路径,加一个path数组,在循环时记录路径即可,再dfs求整个路径,在回溯时输出;
上代码
dfs输出函数的代码
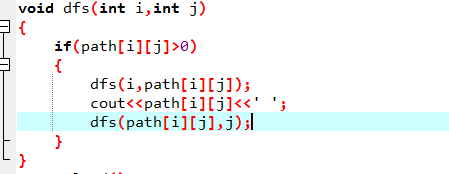
这就是最短路的模板,下去要仔细理解一下算法的深意!!!
