图论——差分约束

• dfs判环
• 差分约束大致理解
• 例题

dfs判环

判环的方法不止有dfs，还是上次讲的拓扑排序，dfs判环的话，需要一个数组来记录一下即可，被遍历过的记为1，在遍历前判断一下，如果为1说明有环，因为你遍历到了已经遍历过的节点，这样的思路实现就很简单了。

代码

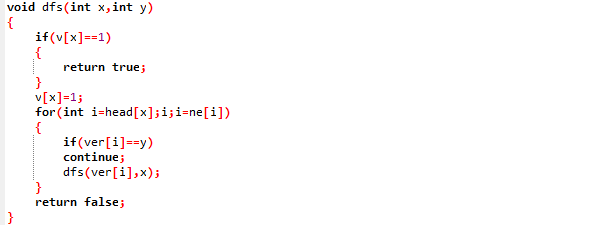
代码实现比较简单，仔细理解。

差分约束大致理解

所谓差分约束即差分和约束，通俗一点的理解也就是做差所得到的约束条件，这也就可以联想到数学当中的不等式了，例如a-b<c，这就是做差得到的小于c的约束条件，通俗意义上来讲这就是差分约束。这个不等式又会使我们联想到另一个东西，最短路不等式d[ver[i]]>d[x]+edge[i];咱们可以把那个a-b<c看成最短路，那其他不等式呐？不等式是可以转换的，都可以换成这种类似的格式，算到这就可以发现，差分约束也就是最短路或最长路。遇到差分约束的题可以往最短路或最长路那方面想。

例题

题目

题面描述

输入输出格式

输入输出

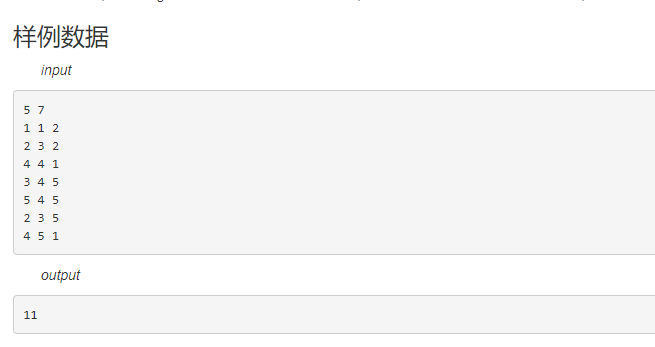
数据范围

这个题就是典型的差分约束题，有五个约束条件，在建图时直接判断建图就好

1.A=B.

2.A<B.

3.A>=B.

4.A>B.

5.A>=B.

这是五个条件，根据这五个条件分别来建图

若A=B，则建一条A与B之间的权值为0的无向边.

若A>B，则建一条B到A的权值为1的有向边.

若A<B，同理，建一条A到B的权值为1的有向边.

若A>=B，建一条B到A的权值为0的有向边.

若A<=B，建一条A到B的权值为1的有向边.

然后再来一个判环就搞定了，最后把最短路值加起来就好了

记得加一个万能原点

建图代码

根据上述分析直接建图即可

spfa求最短路+判环

最后上完整代码

#include<bits/stdc++.h>
using namespace std;
const int io=100000000;
const int oi=1000010;
int ver[oi],head[oi],ne[oi],d[oi],edge[oi],c[oi],tot=0;
long long sum=0;
bool v[oi];
int n,m;
void add(int x,int y,int z)
{
	ver[++tot]=y;
	edge[tot]=z;
	ne[tot]=head[x];
	head[x]=tot;
}
queue<int>q;
bool spfa(int s)
{
	v[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		v[now]=0;
		for(int i=head[now];i;i=ne[i])
		{
			int y=ver[i],z=edge[i];
			if(d[y]<d[now]+z)
			{
				d[y]=d[now]+z;
				c[y]++;
//				cout<<c[y]<<' ';
				if(c[y]>=n)
				return true;
				if(!v[y])
				{
					v[y]=1;
					q.push(y);
				}
			}
		}
	}
	return false;
}
int main()
{
	freopen("candy.in","r",stdin);
	freopen("candy.out","w",stdout);
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		if(x==1)
		{
			add(y,z,0);
			add(z,y,0);
		}
		if(x==2)
		{
			add(y,z,1);
			if(y==z)
			{
				cout<<-1;
				return 0;
			}
		}
		if(x==3)
		{
			add(z,y,0);
		}
		if(x==4)
		{
			add(z,y,1);
			if(y==z)
			{
				cout<<-1;
				return 0;
			}
		}
		if(x==5)
		{
			add(y,z,0);
		}
	 } 
	 for(int i=n;i>=1;i--)
	 add(0,i,1);
//	 for(int i=0;i<=n;i++)
//	 cout<<edge[i]<<' ';
	 if(spfa(0))
	 cout<<-1;
	 else
	 {
	 	for(int i=1;i<=n;i++)
	 	sum+=(long long)d[i];
	 	cout<<sum;
	 }
	return 0;
}