例题
Accumulation Degree
题面描述
树木是自然景观的重要组成部分,因为它们可以防止侵蚀,并在树叶内和树叶下提供特定的保护性生态系统。还发现树木在产生氧气和减少大气中的二氧化碳以及缓和地面温度方面发挥着重要作用。它们也是园林绿化和农业的重要元素,既有美学吸引力,也有果园作物(如苹果)。树木是一种常见的建筑材料。
树木在世界上许多神话中也扮演着密切的角色。许多学者都对寻找树木的特殊属性感兴趣,例如树的中心,树木计数,树木着色。
A(x)A(x) 是这样的属性之一,A(x)A(x)(节点xx的累积度)定义如下:
1. 树的每个边都具有正容量。
2. 树中度为1的节点被命名为终端。
3. 每条边的流量不能超过其容量。
4. A(x)A(x) 是节点x可以流到其他终端节点的最大流量。
由于可能很难理解定义,因此下面显示了一个示例:

| A(1)= 11 + 5 + 8 = 24 | ||
|---|---|---|
| details: | 1 – > 2 | 11 |
| 1 – > 4 – > 3 | 5 | |
| 1 – > 4 – > 5 | 8(因为1 – > 4的容量为13) | |
| A(2)= 5 + 6 = 11 | ||
| details: | 2 – > 1 – > 4 – > 3 | 5 |
| 2 – > 1 – > 4 – > 5 | 6 | |
| A(3)= 5 | ||
| details: | 3 – > 4 – > 5 | 5 |
| A(4)= 11 + 5 + 10 = 26 | ||
| details: | 4 – > 1 – > 2 | 11 |
| 4 – > 3 | 5 | |
| 4 – > 5 | 10 | |
| A(5)= 10 | ||
| details: | 5 – > 4 – > 1 – > 2 | 10 |
树的累积度是其节点之间的最大累积度。在这里,您的任务是找到给定树木的累积度。
输入格式
输入的第一行是整数T,表示测试用例的数量。每个测试用例的第一行是正整数n。以下n -1行中的每一行包含由空格分隔的三个整数x,y,z,表示在节点x和节点y之间存在边,并且边的容量为z。节点编号从1到n。 所有元素都是非负整数,不超过200000.您可以假设测试数据都是树度量。
输出格式
对于每个测试用例,将结果输出到一行。
样例
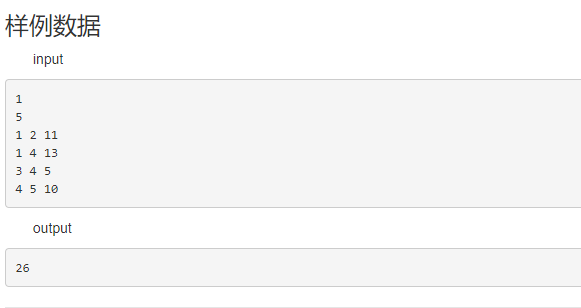
此题的题目甚是难懂,经过hzk大佬讲解才明白题面是什么意思,果然还是我太弱了,看了一下午的背包类树形DP,听他们说很简单,然而我并没有搞定,于是只能默默地转向二次扫描与换根。经过树形DP例题5的历练,这道题和树形例5类似,只是转移的方式不同而已,都是运用了换根。第一次扫描,先找出以1为根的流量最大值,记为数组d[]。再设一个f[x]表示以x为源点,流向整个水系,流量最大是多少,显然是有d[1]==f[1];首先假设f[x]已经被求出,考虑他的子节点y,f[y]还没有被算出,f[y]包括有两部分:
1、从y流向以y为根的子树的最大流量,已经计算并保存在d[y]中。
2、以y沿着到父节点x的河道,进而流向水系中其他部分的流量。
因为以x为源点的总流量为f[x],从x流向y的流量为min(d[y],c(x,y)),所以从x流向除y以外其他部分的流量就是二者的差,然后我们可以运用换根,以y为源点,先流向x,用这个差与c(x,y)取最小值,当度数为1时要进行特殊判断。
标记c(x,y)是x与y的边权。现在再来补一下d[]是怎么来求得。根据题意,要找流量最大的,但是河道的流量不能超过所有河道的最小值,所有要找一下最小值,不能是光找最小值,而是还有流过的要记录。而且在度数等于1时还是要特殊判断,当度数等于1时说明是叶子节点,所以,直接等于边权值就好。
代码
#include<bits/stdc++.h>
using namespace std;
const int oi=2000010;
int ver[oi],head[oi],ne[oi],f[oi],edge[oi],d[oi],tot=0,de[oi],n,sum=0;
bool v[oi];
void add(long long x,long long y,long long z)
{
ver[++tot]=y;
edge[tot]=z;
ne[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
v[x]=1;
d[x]=0;
for(int i=head[x];i;i=ne[i])
{
if(v[ver[i]])
continue;
dfs1(ver[i]);
if(de[ver[i]]==1)
d[x]+=edge[i];
else
d[x]+=min(d[ver[i]],edge[i]);
}
}
void dfs2(int x)
{
v[x]=1;
for(int i=head[x];i;i=ne[i])
{
if(v[ver[i]])
continue;
if(de[x]==1)
f[ver[i]]=d[ver[i]]+edge[i];
else
f[ver[i]]=d[ver[i]]+min(f[x]-min(d[ver[i]],edge[i]),edge[i]);
dfs2(ver[i]);
}
}
int main()
{
// freopen("degree.in","r",stdin);
// freopen("degree.out","w",stdout);
int t;
scanf("%d",&t);
while(t--)
{
// memset(ver,0,sizeof(ver));
// memset(edge,0,sizeof(head));
// memset(head,0,sizeof(head));
// memset(f,0,sizeof(f));
// memset(d,0,sizeof(d));
// memset(ne,0,sizeof(ne));
// memset(v,0,sizeof(v));
// memset(de,0,sizeof(de));
for(int i=1;i<=n;i++)
ver[i]=head[i]=edge[i]=f[i]=d[i]=ne[i]=v[i]=de[i]=0;
tot=0;
scanf("%d",&n);
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
de[x]++;
de[y]++;
}
dfs1(1);
for(int i=1;i<=n;i++)
cout<<d[i]<<' ';
cout<<endl;
memset(v,0,sizeof(v));
f[1]=d[1];
dfs2(1);
for(int i=1;i<=n;i++)
cout<<f[i]<<' ';
cout<<endl;
int ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,f[i]);
printf("%d\n",ans);
}
return 0;
}
