树形DP例4

题面描述

大神hkhh给定⼀棵n个点的边权树，由于他太强了，所以他想考考你。

求每一个以i为根节点的子树中以i为起点的最长链和次长链是多少？（修改来自rfy）

注： 最长链和次长链必须是彼此没有相同边的两条独立的链。

输入格式

第一行输入一个T((1<<T)≤220)T((1<<T)≤220)，表示有T组数据

对于每组数据，输入总共n行 。 第一行有两个整数n和S，分别表示总点数和树根。

第2 ~ n行每行有3个整数x,y,z，表示x到y有一条边，边权为z(0<=z<=10000)。

输出格式

输出总共T*2行

对于每组数据，输出两行

第一行输出n个数，第i个数表示以i号点作为根节点的子树的以i为起点的最长链，数之间用2个空格隔开

第二行输出n个数，第i个数表示以i号点作为根节点的子树的以i为起点的次长链，数之间用2个空格隔开

样例

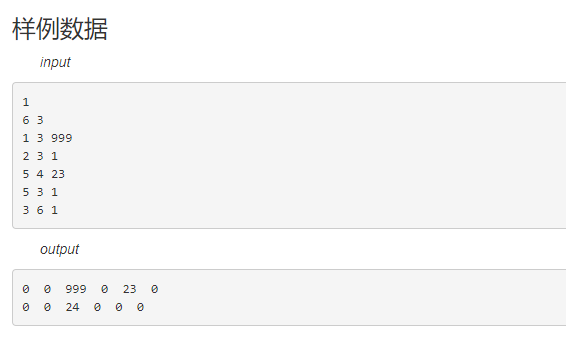
数据范围

这个和求次短路有点像，都是多设一个数组去记录路径，这个主要思路是先dfs遍历所有节点，在回溯的时候判断出最长链和次长链，记录一下就好。这个主意又是一个树上应用。

代码

#include<bits/stdc++.h>
using namespace std;
const int oi=1000010;
int ver[oi],head[oi],ne[oi],d1[oi],edge[oi],d2[oi],tot=0;
void add(int x,int y,int z)
{
	ver[++tot]=y;
	edge[tot]=z;
	ne[tot]=head[x];
	head[x]=tot;
}
void dfs(int x,int y)
{
	for(int i=head[x];i;i=ne[i])
	{
		if(ver[i]==y)
		continue;
		dfs(ver[i],x);
		if(d1[x]<d1[ver[i]]+edge[i])
		{
			d2[x]=d1[x];
			d1[x]=d1[ver[i]]+edge[i];
		}
		else if(d2[x]<d1[ver[i]]+edge[i])
		{
			d2[x]=d1[ver[i]]+edge[i];
		 } 
	}
}
int main()
{
	freopen("T4.in","r",stdin);
	freopen("T4.out","w",stdout);
	int n,k,t;
	scanf("%d",&t);
	while(t--)
	{
		memset(ver,0,sizeof(ver));
		memset(head,0,sizeof(head));
		memset(ne,0,sizeof(ne));
		memset(edge,0,sizeof(edge));
		memset(d1,0,sizeof(d1));
		memset(d2,0,sizeof(d2));
		tot=0;
		scanf("%d%d",&n,&k);
		for(int i=1;i<n;i++)
		{
			int x,y,z;
			scanf("%d%d%d",&x,&y,&z);
			add(x,y,z);
			add(y,x,z);
		}
		dfs(k,0);
		for(int i=1;i<n;i++)
		printf("%d  ",d1[i]);
		printf("%d",d1[n]);
		printf("\n");
		for(int i=1;i<n;i++)
		printf("%d  ",d2[i]);
		printf("%d",d2[n]);
		printf("\n");
	}
	
	return 0;
}