树形DP例5

题面描述

给定一棵n个节点的树，求其中每个点到其他节点的距离和。

输入格式

第一行一个整数n； 接下来n-1行是三个数x,y,z，表示x到y有一条长度为z的边； 数据保证给出的是一棵树。

输出格式

n行，一行一个数，第i行数字表示点i到其他点的距离和。

样例

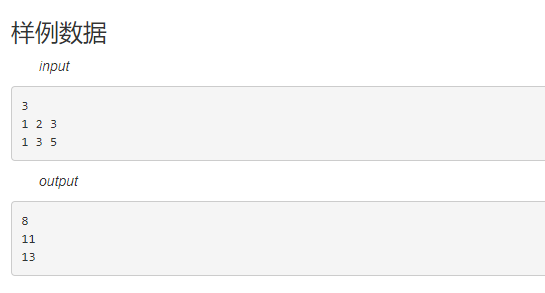
数据范围

这个题需要用到二次扫描和换根法，朴素做法是先以1为根来找，在以2……n，这样明显会超时的，所以，我们可以先预处理出来一个以1为根到所有点距离和，然后我们可以跟据树的特性，我们可以发现，你每找到相邻的节点，都是和上一个节点存在一个关系，你会发现相邻的两个节点到每个点的距离和只有一条边会发生变化，减去少走的遍数并且加上多走的遍数，就是这个点的距离和，假设x与y相邻，(n-2*si[x])这个就是y比x多出来的边数，然后依次枚举一下就好，基本思想还是二次扫描和换根。

代码

#include<bits/stdc++.h>
using namespace std;
long long  si[1001000],de[1001000],head[1001000],ver[1001000],ne[1001000],tot=0,b[1001000],n,k,edge[1001000];
void add(long long x,long long y,long long z)
{
	ver[++tot]=y;
	edge[tot]=z;
	ne[tot]=head[x];
	head[x]=tot;
 } 
void dfs(long long x,long long y)
{
	for(long long i=head[x];i;i=ne[i])
	{
		if(ver[i]==y)
		continue;
		dfs(ver[i],x);
		si[x]+=si[ver[i]];
		b[x]+=b[ver[i]]+edge[i]*si[ver[i]];
	}
}
void dfs2(long long x,long long fa,long long s)	
{
	if(x!=1)
	de[x]=de[fa]+(n-2*si[x])*s;//仔细理解一下(n-2*si[x])是怎么来的
	for(long long i=head[x];i;i=ne[i]) {
		long long v=ver[i];
		if(v==fa)
		continue;
		dfs2(v,x,edge[i]);
	}                   
}
int main()
{
	freopen("t5.in","r",stdin);
	freopen("t5.out","w",stdout);
	scanf("%lld",&n);
	for(long long i=1;i<n;i++)
	{
		long long x,y,z;
		scanf("%lld%lld%lld",&x,&y,&z);
		add(x,y,z);
		add(y,x,z);
	}
	for(long long i=1;i<=n;i++)
	si[i]=1;
	dfs(1,0);
	de[1]=b[1];
	dfs2(1,0,0);
	for(long long i=1;i<=n;i++)
	{
		printf("%lld\n",de[i]);
	}
	return 0;
}

de[x]=de[fa]+(n-2si[x])s;//仔细理解一下(n-2*si[x])是怎么来的，是-si[x]+(n-si[x])合并出来的