树形DP——基础

所谓树形DP，就是在树上的DP。线性DP是在线上进行DP，进行无后效性的状态转移。树形DP就是在树上以节点从深到浅（子树从小到大）的顺序作为DP的“阶段”。我们通常采用递归的方式来实现树形DP，先递归到每个子节点然后在回溯的时候从子节点再向父节点进行状态转移。

没有上司的舞会

题面描述

Ural大学有N个职员，编号为1~N。他们有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。每个职员有一个快乐指数。现在有个周年庆宴会，要求与会职员的快乐指数最大。但是，没有职员愿和直接上司一起与会。

输入格式

第一行一个整数N。(1<=N<=6000)

接下来N行，第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)

接下来N-1行，每行输入一对整数L,K。表示K是L的直接上司。

最后一行输入0,0。

输出格式

输出最大的快乐指数。

样例

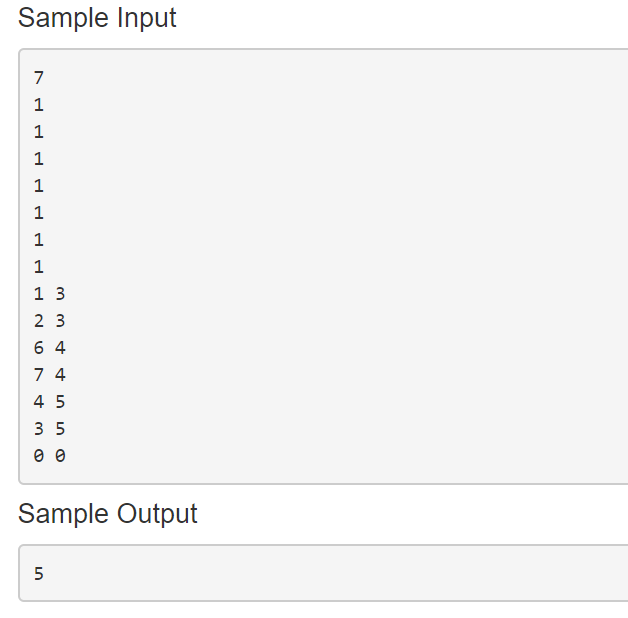
此题因为是树形DP，肯定是不能去想搜索的，死扣树形DP的定义，先递归到所有的子节点，然后在回溯的时候进行状态转移。例如这道题，题目描述说，不能和自己的上司一起跳舞，也就是说不能和自己的父亲节点同时选上，从这里可以分析出来，有两种状态，一是选自己的父亲，不选儿子，二是选自己的儿子不选父亲。这样就可以大致写出状态转移方程，f[]表示不选父亲，g[]表示选父亲。

1、以x为根，并且x不参加舞会，来回溯最大快乐值

f[x]=max(f[y],g[y]);//y表示子节点

2、以x为根，并且x参加舞会，来回溯最大快乐值

g[x]=a[x]+f[y];

DP题既然状态转移方程出来了，代码也就呼之欲出了

#include<bits/stdc++.h>
using namespace std;
const int oi=2000010;
long long ver[oi],head[oi],ne[oi],f[oi],edge[oi],a[oi],tot=0,g[oi],n,sum=0;
bool v[oi];
void add(long long x,long long y)
{
	ver[++tot]=y;
	ne[tot]=head[x];
	head[x]=tot;
}
void dfs(int x)
{
	for(int i=head[x];i;i=ne[i])
	{
		dfs(ver[i]);
		f[x]+=max(f[ver[i]],g[ver[i]]);
		g[x]+=f[ver[i]];
	}
	g[x]+=a[x];
}
int main()
{
//	freopen("test.in","r",stdin);
//	freopen("test.out","w",stdout);
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<n;i++)
	{
		int x,y;
		cin>>x>>y;
		v[x]=1;
		add(y,x);
	}
	int p;
	for(int i=1;i<=n;i++)
	if(!v[i])
	{
		p=i;
		break;
	}
	dfs(p);
	cout<<max(f[p],g[p]);
	return 0;
}