选课+输出方案

题面描述

学校实行学分制。每门的必修课都有固定的学分，同时还必须获得相应的选修课程学分。学校开设了N（N < 500）门的选修课程，每个学生可选课程的数量M是给定的。学生选修了这M门课并考核通过就能获得相应的学分。

　　在选修课程中，有些课程可以直接选修，有些课程需要一定的基础知识，必须在选了其它的一些课程的基础上才能选修。例如《Frontpage》必须在选修了《Windows操作基础》之后才能选修。我们称《Windows操作基础》是《Frontpage》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。每门课都有一个课号，依次为1，2，3，…。 例如:

上例中1是2的先修课，即如果要选修2，则1必定已被选过。同样，如果要选修3，那么1和2都一定已被选修过。 　　你的任务是为自己确定一个选课方案，使得你能得到的学分最多，并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。

输入格式

第一行包括两个正整数N、M（中间用一个空格隔开）其中N表示待选课程总数（1≤N≤500)，M表示学生可以选的课程总数（1≤M≤N)。 以下M行每行代表一门课，课号依次为1，2,…,M。每行有两个数（用一个空格隔开），第一个数为这门课的先修课的课号（若不存在先修课则该项为0），第二个数为这门课的学分。

输出格式

第一行只有一个数，即实际所选课程的学分总数。 以下M行每行有一个数，表示学生所选课程的课号。

M行学生选课的课号按从小到大的顺序输出。

样例

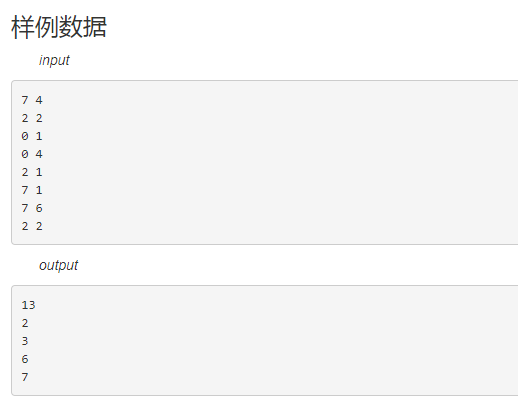
这个题用到了一个方法，多叉树转二叉树，，这样的话在输出答案的时候会简单一些，状态转移方程f[x][y]=max(f[x][y],max(f[br[x]][y],f[br[x]][i]+f[ch[x]][y-i-1]+a[x]));br[]是兄弟数组，ch[]是儿子数组，左儿子右兄弟法，用这个方法来遍历，在回溯是记录一下答案，输出方案的话，和那样遍历方式一样，如果找到一个相等的就接着遍历那一个，一直往下走，要仔细理解一下遍历的方法，还有状态转移方程的得出。

代码

#include<bits/stdc++.h>
using namespace std;
int f[5000][5000],br[200010],ch[200010],a[200010],ans[200010];
void dfs1(int x,int y)
{
	if(f[x][y]>=0)
	return;
	if(!x||!y)
	{
		f[x][y]=0;
		return;
	}
	dfs1(br[x],y);
	for(int i=0;i<=y-1;i++)
	{
		dfs1(br[x],i);
		dfs1(ch[x],y-i-1);
		f[x][y]=max(f[x][y],max(f[br[x]][y],f[br[x]][i]+f[ch[x]][y-i-1]+a[x]));
	}
}
void dfs2(int x,int y)
{
	if(!x||!y)
	{
		return;
	}
	if(f[x][y]==f[br[x]][y])
	dfs2(br[x],y);
	else
	for(int i=0;i<=y-1;i++)
	{
		if(f[x][y]==f[br[x]][i]+f[ch[x]][y-i-1]+a[x])
		{
			dfs2(br[x],i);
			dfs2(ch[x],y-i-1);
			ans[x]=1;
			return;
		}
	}
}
int main()
{
	freopen("course.in","r",stdin);
	freopen("course.out","w",stdout);
	int n,m;
	cin>>n>>m;
	memset(f,-1,sizeof f);
	for(int i=1;i<=n;i++)
	{
		int x,y;
		cin>>x>>a[i];
		if(!x)
		x=n+1;
		br[i]=ch[x];
		ch[x]=i;
	}
	dfs1(ch[n+1],m);
	cout<<f[ch[n+1]][m]<<endl;
	dfs2(ch[n+1],m);
	for(int i=1;i<=n;i++)
	if(ans[i])
	cout<<i<<endl;
}