computer

题面描述

一所学校前一段时间买了第一台计算机（所以这台计算机的ID是1）。

近年来，学校又购买了N-1台新计算机。

每台新计算机都与之前买进的计算机中的一台建立连接。

现在请你求出第i台计算机到距离其最远的计算机的电缆长度。

例如，上图中距离计算机1最远的是计算机4，因此 S1=3S1=3；距离计算机2最远的是计算机4和5，因此 S2=2S2=2；距离计算机3最远的是计算机5，所以 S3=3S3=3；同理，我们也得到 S4=4，S5=4S4=4，S5=4。

输入格式

每组测试数据第一行包含整数N。

接下来N-1行，每行包含两个整数，第 i 行的第一个整数表示第 i 台电脑买入时连接的电脑编号，第二个整数表示这次连接花费的电缆长度。

输出格式

每组测试数据输出N行。

第 i 行输出第 i 台电脑的 Si。

样例

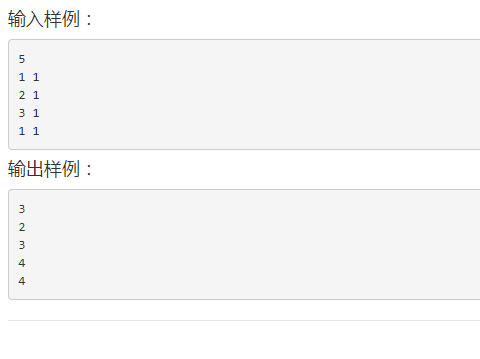
数据范围

这个题看一眼数据范围，就能知道朴素做法一定是超时的，只能想一下怎么去优化，咱们可以找一下换根的转移方程。我们可以把1的最远距离和次远距离求出来，然后进行遍历，这里有两种情况，1、最长路过这个节点；2、最长路不过这个节点；如果过这个节点的话，那咱们就走次长路，如果不过，就直接走最长路即可

代码

#include<bits/stdc++.h>
using namespace std;
const int oi=2000010;
int ver[oi],head[oi],edge[oi],ne[oi],d1[oi],d2[oi],d3[oi],ans[oi],tot=0;
void add(int x,int y,int z)
{
	ver[++tot]=y;
	edge[tot]=z;
	ne[tot]=head[x];
	head[x]=tot;
}
void dfs1(int x,int y)
{
	for(int i=head[x];i;i=ne[i])
	{
		if(ver[i]==y)
		continue;
		dfs1(ver[i],x);
		if(d1[x]<d1[ver[i]]+edge[i])
		{
			d2[x]=d1[x];
			d1[x]=d1[ver[i]]+edge[i];
		}
		else 
		{
			d2[x]=max(d2[x],d1[ver[i]]+edge[i]);
		} 
	}
}
void dfs2(int x,int y)
{
	for(int i=head[x];i;i=ne[i])
	{
		if(ver[i]==y)
		continue;
		if(d1[x]==d1[ver[i]]+edge[i])
		{
			d3[ver[i]]=max(d2[x],d3[x])+edge[i];
		}
		else
		d3[ver[i]]=max(d1[x],d3[x])+edge[i];
		ans[ver[i]]=max(d3[ver[i]],d1[ver[i]]);
		dfs2(ver[i],x);
	}
}
int main()
{
	freopen("computer.in","r",stdin);
	freopen("computer.out","w",stdout); 
	int n;
	scanf("%d",&n);
	for(int i=2;i<=n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(i,x,y);
		add(x,i,y);
	}
	dfs1(1,0);
//	for(int i=1;i<=n;i++)
//    cout<<d1[i]<<' ';
//    cout<<endl;
//    for(int i=1;i<=n;i++)
//    cout<<d2[i]<<' ';
//    cout<<endl;
	ans[1]=d1[1];
	dfs2(1,0);
	for(int i=1;i<=n;i++)
	printf("%d\n",ans[i]);
}