题面描述
Flappy Bird是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。为了简化问题,我们对游戏规则进行了简化和改编:
游戏界面是一个长为 nn,高为 mm 的二维平面,其中有 kk 个管道(忽略管道的宽度)。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为 11,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 XX,每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 YY。小鸟位于横坐标方向不同位置时,上升的高度 XX 和下降的高度 YY 可能互不相同。
小鸟高度等于 00 或者小鸟碰到管道时,游戏失败。小鸟高度为 mm 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
在此配个acwing的图

输入格式
第 11 行有 33 个整数 n, m, kn,m,k,分别表示游戏界面的长度,高度和水管的数量,每两个整数之间用一个空格隔开;
接下来的 nn 行,每行 22 个用一个空格隔开的整数 XX 和 YY,依次表示在横坐标位置 0 \sim n-10∼n−1 上玩家点击屏幕后,小鸟在下一位置上升的高度 XX,以及在这个位置上玩家不点击屏幕时,小鸟在下一位置下降的高度 YY。
接下来 k行,每行 3 个整数 P, L, H每两个整数之间用一个空格隔开。每行表示一个管道,其中 P 表示管道的横坐标,L 表示此管道缝隙的下边沿高度,H 表示管道缝隙上边沿的高度(输入数据保证 P 各不相同,但不保证按照大小顺序给出)。
输出格式
共两行。
第一行,包含一个整数,如果可以成功完成游戏,则输出 11,否则输出 00。
第二行,包含一个整数,如果第一行为 11,则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
样例
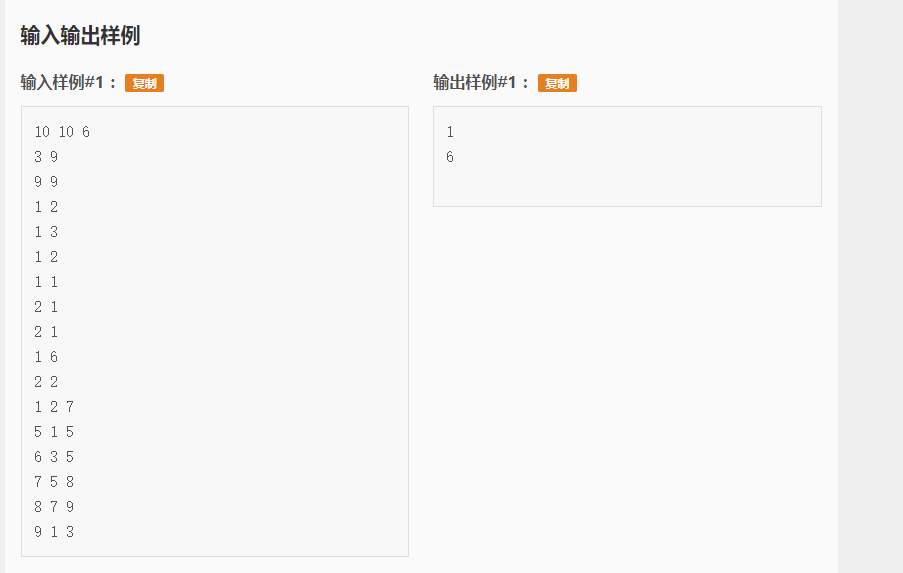
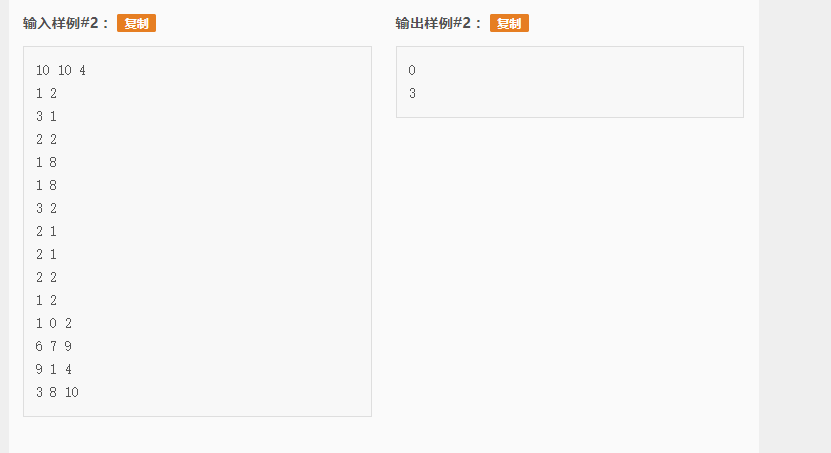
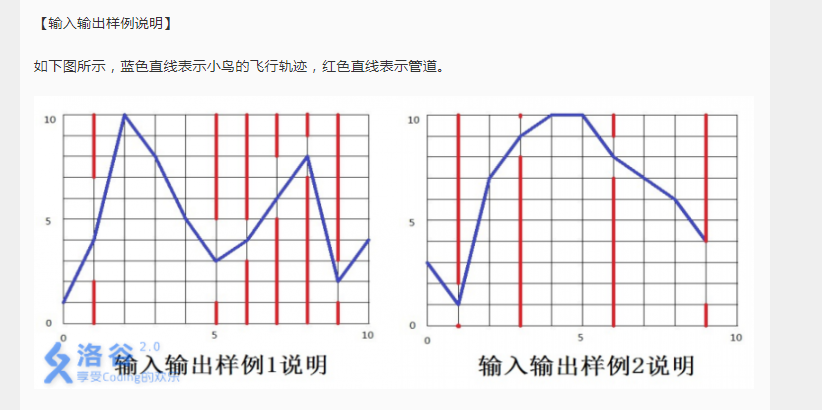
样例解释
数据范围

这是一道DP题,题面有一点难懂,NOIP都是这种题,只能练习语文能力了QAQ。由题意可知,一个时刻内可以进行多次跳跃,但是下降只能进行一次,DP方程是可以很轻易的得到的,刚开始我发现有两种情况,先设f[i][j],代表在第i列上达到j高度需要的最少点击数f[i][j]=min(f[i-1][j-k*x[i-1]]+1,f[i][j]);这是由上一列点了k次,上升了k*x[i-1]高度到达了j,还有一种就是f[i][j]=min(f[i][j],f[i-1][j+y[i-1]]);但是这是显然没有想全面的,还有到达m或超过m全部都算在顶飞,并不会死,所以,要特判顶端,并且还有一种很怪异的判断,就是意思上是直上直下的飞,因为这是一个没有速度概念的,你只要手速快,可以视为智商直下平移到上一条线,在洛谷里如果没有这个判断你会痛失50%的数据,WA到你怀疑人生。还有在最后一点如果不行的话,在找过了几个柱子的时候是要从n……1,这样循环比较好判断,发现有一个合法就直接输出就好了,还有在减柱子数的时候还有判断一下这个上面是否有柱子,如果没有的话就不用去减,没有这个判断会多减。
代码
#include<bits/stdc++.h>
using namespace std;
const int inf=10000000000;
int f[10100][1010],op1[1200010],op2[100010],x[100010],y[100010];
int main()
{
int n,m,k;
cin>>n>>m>>k;
for(int i=0;i<n;i++)
{
cin>>x[i]>>y[i];
}
for(int i=1;i<=n;i++)
{
op1[i]=0;
op2[i]=m+1;
}
for(int i=1;i<=k;i++)
{
int l;
cin>>l;
cin>>op1[l]>>op2[l];
}
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
f[i][j]=inf;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(j>=x[i-1])
{
f[i][j]=min(f[i][j],f[i-1][j-x[i-1]]+1);
f[i][j]=min(f[i][j],f[i][j-x[i-1]]+1);
}
if(j==m)
{
for(int k=j-x[i-1];k<=m;k++)
{
f[i][j]=min(f[i][j],f[i-1][k]+1);
f[i][j]=min(f[i][j],f[i][k]+1);
}
}
}
for(int j=op1[i]+1;j<op2[i];j++)
{
if(j+y[i-1]<=m)
{
f[i][j]=min(f[i][j],f[i-1][j+y[i-1]]);
}
}
for(int j=1;j<=op1[i];j++)
f[i][j]=inf;
for(int j=op2[i];j<=m;j++)
f[i][j]=inf;
}
// for(int i=1;i<=n;i++)
// {
// for(int j=0;j<=m;j++)
// cout<<f[i][j]<<' ';
// cout<<endl;
// }
int minn=inf;
for(int i=1;i<=m;i++)
{
minn=min(minn,f[n][i]);
}
if(minn<inf)
{
cout<<1<<endl<<minn<<endl;
}
else
{
cout<<0<<endl;
int ll=k;
for(int i=n;i>=1;i--)
{
int ans=inf;
for(int j=op1[i]+1;j<op2[i];j++)
{
ans=min(ans,f[i][j]);
}
if(ans!=inf)
{
cout<<ll<<endl;
return 0;
}
if(op2[i]<=m)
ll--;
}
}
}