Naptime

题目描述

rainbow给了freda N秒的自由活动时间，不过由于刚刚游览城堡有些累了，freda只想花B秒的时间来卖萌，剩下的时间她要在rainbow的城堡里睡个好觉好好休息一下。

rainbow给这N秒每秒定义了一个值Ui，如果第i秒钟freda在卖萌，那么她可以获得Ui点卖萌指数lala~

freda开始卖萌后可以随时停止，休息一会儿之后再开始。不过每次freda开始卖萌时，都需要1秒来准备= =，这一秒是不能获得卖萌指数的。当然，freda卖萌和准备的总时间不能超过B。

更特殊的是，这N秒钟时间是环形的。也就是freda可以从任意时间开始她的自由活动并持续N秒。

为了使自己表现得比水叮当更萌，现在freda想知道，她最多能获得多少卖萌指数呢？

输入格式

第一行包含两个整数N和B。

第2~N+1行每行一个整数，其中第i+1行的整数表示Ui。

输出格式

输出一个整数，表示freda可以获得的最大卖萌指数。

样例

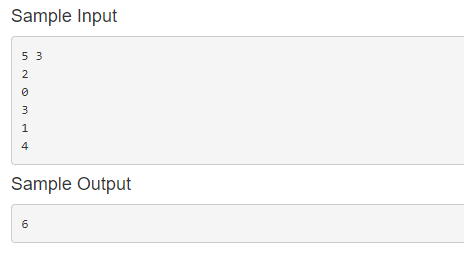
数据范围

环形与后效性的处理这个就是要把环形断开，转化成线性，可以避免环形不必要的dfs枚举。这个题就是可以找n与1的地方断开，转化成两个问题，一个是1是不可能在休息的，二就是1一定是在休息的，这样就可以覆盖了整个问题。设f[i][j][1]表示前i个小时休息了j个小时，并且第i个小时正在休息， f[i][j][0]表示前i个小时休息了j个小时，并且第i个小时不在休息，然后列出DP方程

f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]);

f[i][j][1]=max(f[i-1][j-1][0],f[i-1][j-1][1]);

这是第一个问题的DP方程，初始化f[1][0][0]=0,f[1][1][1]=0;

接下来说一下第二个问题的DP方程，我们可以发现，两个问题的本质其实是一样的，只不过不同的只是初始化的时候不一样而已，第一个是0，而第二个初始化为a[i]，再用上一个问题的DP方程解一遍找个最大值就好了。

代码

#include<bits/stdc++.h>
using namespace std;
int f[4000][4000][3],a[5000],maxx=-1000000000;
int main()
{
	freopen("naptime..in","r",stdin);
	freopen("naptime..out","w",stdout);
	int n,b;
	cin>>n>>b;
	memset(f,-10,sizeof(f));
	for(int i=1;i<=n;i++)
	cin>>a[i];
	f[1][1][1]=0;
	for(int i=1;i<=n;i++)
	f[i][0][0]=0;
	for(int i=2;i<=n;i++)
	{
		for(int j=1;j<=b;j++)
		{
			f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]);
			f[i][j][1]=max(f[i-1][j-1][0],f[i-1][j-1][1]+a[i]);
		}
	}
	maxx=max(f[n][b][0],f[n][b][1]);
	memset(f,-10,sizeof(f));
	f[1][1][1]=a[1];
	for(int i=2;i<=n;i++)
	{
		for(int j=1;j<=b;j++)
		{
			f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]);
			f[i][j][1]=max(f[i-1][j-1][0],f[i-1][j-1][1]+a[i]);
		}
	}
	maxx=max(maxx,f[n][b][1]);
	cout<<maxx;
}