The Crazy Tree

题面描述

给定一棵 n 个结点的树，结点编号为 1~n，i 号结点的权重记为 wi（每个点的权值各不相同）。我们定义一个“疯子树”为： 1. 是一个联通子图。 2. 我们将子图内的点按照权重从小到大排序后序列为 b1,b2,…,bm，对于任意的i(i<m),bi到bi+1。最短路径（不含bi和bi+1）上的结点的权值都小于等于wbi。输出包含结点最多的“疯子树”的结点数。

输入格式

数据有多组 case,文件以 EOF 结束，每组第一行输入一个 n 表示树的节点数；

接下来一行包含 n 个整数，第 i 个数表示 i 号结点的权重wi；

接下行 n-1 行，第i行包含 2 个整数 ui, vi，表示ui和vi有一条边。

输出格式

对于每组 case 输出一行，包含一个整数，表示包含结点最多的“疯子树”的结点数。

样例

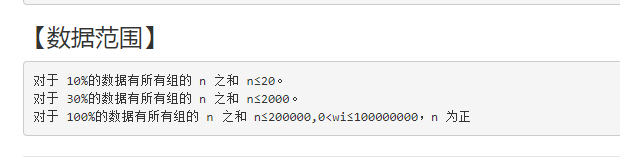
数据范围

这个题我一开始是没有看懂题的QAQ，可能描述的有点抽象，语文不好的我可能没有理解，题目大致意思是这样的，就是给你一棵树，让你找一下含有最多节点的疯子树，何为疯子树？就是满足最短路径（不含bi和bi+1）上的结点的权值都小于等于wbi 。太抽象了，由于这是一棵树，在树上的最短路径是只有一条，而且最短路径也是一棵树，所以并没有题目当中说的那么玄幻，经过画图可以发现，疯子树是类似于谷状，向下凹的，详情请参看博客

https://blog.csdn.net/ShadyPi/article/details/79939717

代码

#include<bits/stdc++.h>
using namespace std;
const int oi=2000010;
int ver[oi],head[oi],edge[oi],f[oi],ne[oi],d1[oi],aj[oi],s[oi],ans[oi],tot=0,sum=0,n,m;
struct hf
{
	int v,id;
}a[oi];
bool cmp(hf o,hf p)
{
	return o.v>p.v;
}
void add(int x,int y)
{
	ver[++tot]=y;
	ne[tot]=head[x];
	head[x]=tot;
}
int main()
{
	freopen("crazy.in","r",stdin);
	freopen("crazy.out","w",stdout);
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		memset(a,0,sizeof(a));
		for(int i=1;i<=n;i++)
		head[i]=ver[i]=ne[i]=ans[i]=0;
		memset(f,0,sizeof(f));
		for(int i=1;i<=n;i++)
		{
			cin>>a[i].v;
			a[i].id=i;
		}
		for(int i=1;i<n;i++)
		{
			int x,y;
			cin>>x>>y;
			add(x,y);
			add(y,x);
		}
		sort(a+1,a+n+1,cmp);
		for(int i=1;i<=n;i++)
		{
			f[a[i].id]=1;
			for(int j=head[a[i].id];j;j=ne[j])
			{
				if(!f[ver[j]])
				ans[ver[j]]+=ans[a[i].id]+1;
			}
		}
		int maxx=0;
		for(int i=1;i<=n;i++)
		maxx=max(maxx,ans[i]);
		cout<<maxx+1<<endl;
	}
}