最短Hamilton路径

题面描述

给定一张 n 个点的带权无向图，点从 0~n-1 标号，求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。

输入格式

第一行输入整数nn。

接下来n行每行n个整数，其中第i行第j个整数表示点ii到jj的距离（记为a[i,j]）。

对于任意的x,y,z，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]>=a[x,z]。

输出格式

输出一个整数，表示最短Hamilton路径的长度。

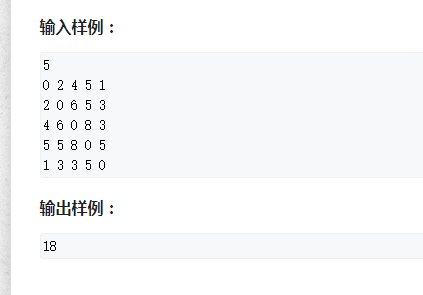
样例

状态压缩，就是把集合个数不超过n，每一个元素都是小于k的自然数，则我们可以把这个集合看做一个n位k进制数，用这一个数来代表其中的一维状态。这是个旅行商问题，暴力的话大约是20！*20，是很大的一个数字，是不符合时限的，所以，我们要对他进行压缩我们把n那层状态看做1<<n位，然后进行遍历，并且我们可以发现，这个是不需要去遍历出所有情况的，我们可以发现我们要的是一个方案最优，而不是输出整个方案，所以，只要记录当前的最优解就好了。用一个2进制数来记录一下状态，因为只有0或1两种状态。

代码

#include<bits/stdc++.h>
using namespace std;
int f[1<<20][50];
int a[50][25];
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        cin>>a[i][j];
    }
    memset(f,0x3f,sizeof(f));
    f[1][0]=0;
    for(int i=0;i<1<<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            if(i>>j&1)
            {
                for(int k=0;k<n;k++)
                {
                    if(i-(1<<j)>>k&1)
                    {
                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+a[k][j]);
                    }
                }
            }
        }
    }
    cout<<f[(1<<n)-1][n-1];
}