种葱

题面描述

初音ミク的土地可以看成是由N个地块组成，由1到N编号，N个地块排成一横排。

鏡音リン提出了a个要求，要求从第l个到第r个地块（包括l和r），葱的总数不能超过v。

鏡音レン提出了b个要求，要求从第l个到第r个地块（包括l和r），葱的总数不能少于v。

同时，因为地块大小的限制，每个地块的葱不能超过k。

现在，初音ミク想知道，满足所有要求的情况下，她最多能种多少葱，最少能种多少葱。

输入格式

第一行两个整数N、k，用空格分开。

第二行一个整数a。

以后a行，每行三个整数l、r、v，用空格分开，意义如题目描述。

下一行一个整数b。

以后b行，每行三个整数l、r、v，用空格分开，意义如题目描述。

输出格式

第一行一个整数，表示葱的最大数目。

第二行一个整数，表示葱的最小数目。

样例

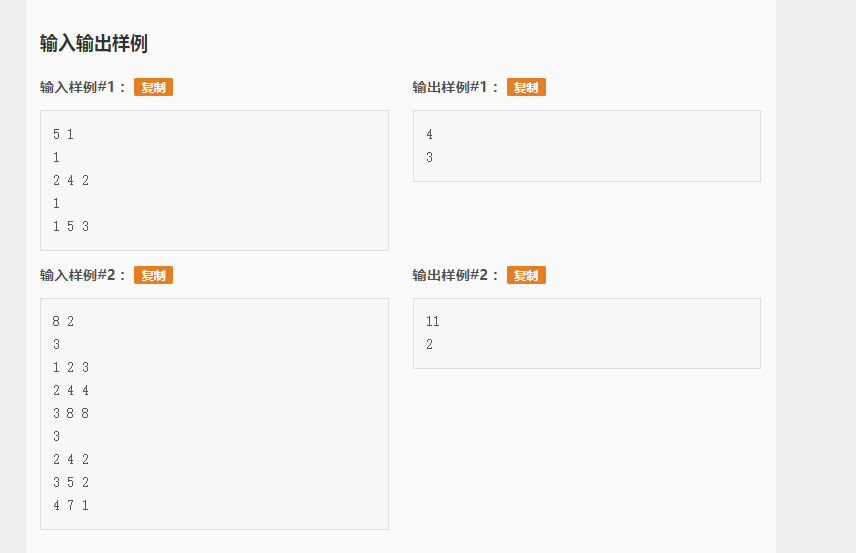
这个题我本来是，没有思路的，可是一看题解，我真的QAQ了，差分约束，我的天哪，我前一段时间刚刚搞过，现在碰到了还是不会，感觉白搞了QAQ，算了，先进入正题。此题他也给出了明确的约束条件，只不过我被区间迷惑了。并没有想到这是差分约束。对于每个i∈[0,N]，建点i表示前i块地的葱的总数。对于每个i∈[1,N]，建边(i-1,i,k)和(i,i-1,0)；k是每块地所能种的最大葱树。对于每个要求[l,r]内的葱不超过v，建边(l-1,r,v)；前缀和思想。对于每个要求[l,r]内的葱不少于v，建边(r,l-1,-v)；建反向边，为了求最小值，这样就不用再新建一个图了，只是自己的理解。 (i,i-1,0) 和 (r,l-1,-v) 是用来求葱数最小用的，所以可以得出结论葱的最大值是从0到N的最短路。葱的最小值是从N到0的最短路的相反数。因为你设的是负边权，这也就是说明了用spfa。

代码

#include<bits/stdc++.h>
using namespace std;
const int oi=100010;
int ver1[oi],head1[oi],ne1[oi],edge1[oi],tot1=0,d1[oi],v1[oi];
int ver2[oi],head2[oi],ne2[oi],edge2[oi],d2[oi],v2[oi];
void add1(int x,int y,int z)
{
	ver1[++tot1]=y;
	edge1[tot1]=z;
	ne1[tot1]=head1[x];
	head1[x]=tot1;
} 
queue<int>q1;
void spfa1(int s)
{
	while(q1.size())
	q1.pop();
	memset(v1,0,sizeof(v1));
	memset(d1,10,sizeof(d1));
	v1[s]=1;
	q1.push(s);
	d1[s]=0;
	while(q1.size())
	{
		int now=q1.front();
		q1.pop();
		v1[now]=0;
		for(int i=head1[now];i;i=ne1[i])
		{
			if(d1[ver1[i]]>d1[now]+edge1[i])
			{
				d1[ver1[i]]=d1[now]+edge1[i];
				if(!v1[ver1[i]])
				{
					v1[ver1[i]]=1;
					q1.push(ver1[i]);
				}
			}
		}
	}
}
int main()
{
	int n,k,a,b;
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		add1(i-1,i,k);
		add1(i,i-1,0);
	}
	cin>>a;
	for(int i=1;i<=a;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		add1(x-1,y,z);
	}
	cin>>b;
	for(int i=1;i<=b;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		add1(y,x-1,-z);
	}
	spfa1(0);
	cout<<d1[n]<<endl;
	spfa1(n);
	cout<<-d1[0]; 
}