跑图

题面描述

happy inf的地图可以看成由N个节点，M条单向道路组成。N个节点的编号由1到N。每条道路有一个长度。路程等于经过的所有道路长度之和。

ck想从s号节点跑到t号节点。他可以使用一次末影珍珠，对于任意一条从u到v的单向道路，可以使用末影珍珠从u瞬移v，瞬移不计算路程。末影珍珠也可以反向使用，即从v瞬移到u，同样不计算路程。

ck想知道，从s到t的最短路的路程。

输入格式

第一行四个整数用空格隔开：N M s t

以后M行，每行三个整数u v l，表示从u到v存在一条长度为l的单向道路。

输出格式

一个整数表示最短路的路程。

样例

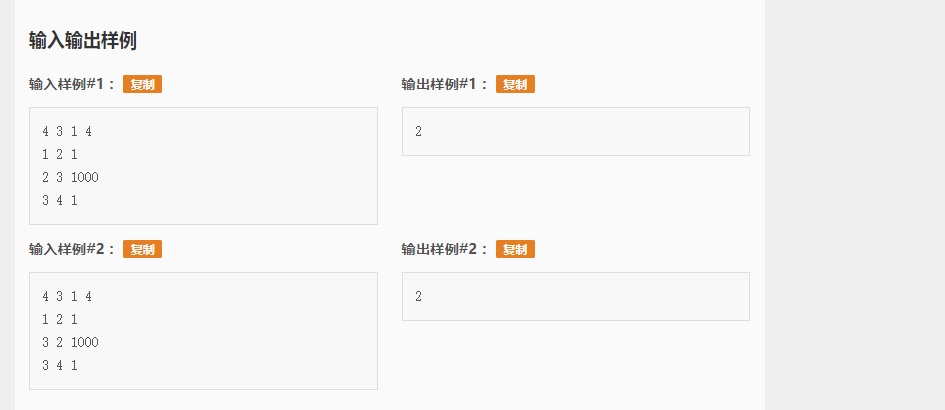
数据范围

这个题吧就是个稍厉害点的最短路，然而我并不会QAQ，只是有了一个技能，有一个结论 ，直接说题解吧，但是我并不知道为什么可以这样写，不知道为什么这样写是对的，所以先写下来再说，先建图，两张，一张正向图，一张反向图，先以s跑正向图，在以t跑反向图再枚举所有的边，因为d1[x]+d2[y]和d1[y]+d2[x]都是合法路径，所以直接找个最小值即可。推翻上述推论，我现在懂了！知道他的正确性了， d1[x]+d2[y] 这个是求正向缺一条边的情况， d1[y]+d2[x] 这个是算反向缺一条边的情况。

代码（自认为题解代码风格有点略丑，放上自己的）

#include<bits/stdc++.h>
using namespace std;
const int oi=100010;
int ver1[oi],head1[oi],ne1[oi],edge1[oi],d1[oi],v1[oi];
int ver2[oi],head2[oi],ne2[oi],edge2[oi],d2[oi],v2[oi];
void add1(int x,int y,int z,int tot1)
{
	ver1[tot1]=y;
	edge1[tot1]=z;
	ne1[tot1]=head1[x];
	head1[x]=tot1;
} 
void add2(int x,int y,int z,int tot2)
{
	ver2[tot2]=y;
	edge2[tot2]=z;
	ne2[tot2]=head2[x];
	head2[x]=tot2;
} 
queue<int>q1;
void spfa1(int s)
{
	v1[s]=1;
	q1.push(s);
	d1[s]=0;
	while(q1.size())
	{
		int now=q1.front();
		q1.pop();
		v1[now]=0;
		for(int i=head1[now];i;i=ne1[i])
		{
			if(d1[ver1[i]]>d1[now]+edge1[i])
			{
				d1[ver1[i]]=d1[now]+edge1[i];
				if(!v1[ver1[i]])
				{
					v1[ver1[i]]=1;
					q1.push(ver1[i]);
				}
			}
		}
	}
}
queue<int>q2;
void spfa2(int s)
{
	v2[s]=1;
	q2.push(s);
	d2[s]=0;
	while(q2.size())
	{
		int now=q2.front();
		q2.pop();
		v2[now]=0;
		for(int i=head2[now];i;i=ne2[i])
		{
			if(d2[ver2[i]]>d2[now]+edge2[i])
			{
				d2[ver2[i]]=d2[now]+edge2[i];
				if(!v2[ver2[i]])
				{
					v2[ver2[i]]=1;
					q2.push(ver2[i]);
				}
			}
		}
	}
}
int main()
{
	memset(d1,0x3f,sizeof(d1));
	memset(d2,0x3f,sizeof(d2));
	int n,m,s,t;
	cin>>n>>m>>s>>t;
	for(int i=1;i<=m;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		add1(x,y,z,i);
		add2(y,x,z,i);
	}
	spfa1(s);
	spfa2(t);
	int minn=1e9;
	for(int i=1;i<=m;i++)
	{
		minn=min(minn,d1[ver1[i]]+d2[ver2[i]]);
		minn=min(minn,d1[ver2[i]]+d2[ver1[i]]);
	}
	cout<<minn;
}