KMP算法

KMP算法是用来快速匹配字符串用的算法，通常用来在O(n)的时间内可以求出模板串在所求的串中的位置。

来大致讲一下KMP，KMP是一个很难理解的东西（我就没有很理解QAQ）不过这不重要，先知道怎么用才是王道。

像yxc大佬说的，在考虑KMP算法的时候，我们一定要先知道朴素做法是什么，在这里，我们先引入一个例题。

KMP字符串

题面描述

给定一个模式串S，以及一个模板串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模板串P在模式串S中多次作为子串出现。

求出模板串P在模式串S中所有出现的位置的起始下标。

输入格式

第一行输入整数N，表示字符串P的长度。

第二行输入字符串P。

第三行输入整数M，表示字符串S的长度。

第四行输入字符串M。

输出格式

共一行，输出所有出现位置的起始下标（下标从0开始计数），整数之间用空格隔开。

样例和数据范围

这个题就是KMP模板题，是KMP的一个应用，就是p在s中出现的起始下标。但是我们需要在O(n)的时间内来完成，朴素做法O(nm)是会超时的，但是我们要先来了解一下朴素做法。朴素做法是怎么来匹配的呐？思考一下，这个应该不是很困难。朴素做法就不加讲解了，直接上代码

void pusu()
{
	for(int i=1;i<=m;i++)
	{
		bool flag=1;
		for(int j=i,k=1;k<=n;j++,k++)
		{
			if(s[j]!=p[k])
			{
				flag=0;
				break;
			}
		}
		if(flag)
		{
			cout<<i<<endl;
		}
	}
}

暴力判断时间复杂度是O(mn)的，所以会超时，那么我们可以来优化，重点是怎么优化，KMP算法是什么。

朴素做法在不匹配的时候会向后挪一位，再从头开始判断，例如下面的图所示

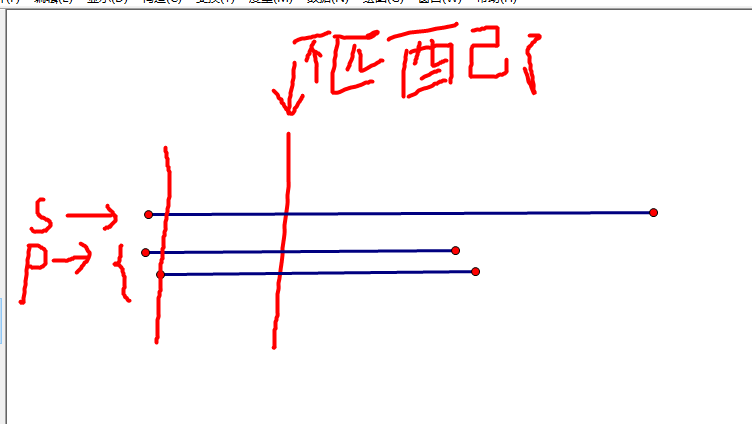
如果不匹配，会向后挪一位然后从头开始判断，但是KMP算法不是这样，KMP算法是先预处理出来一个next数组，来存一下，next数组存的是每个点的后缀与前缀相等的最大长度，如图所示

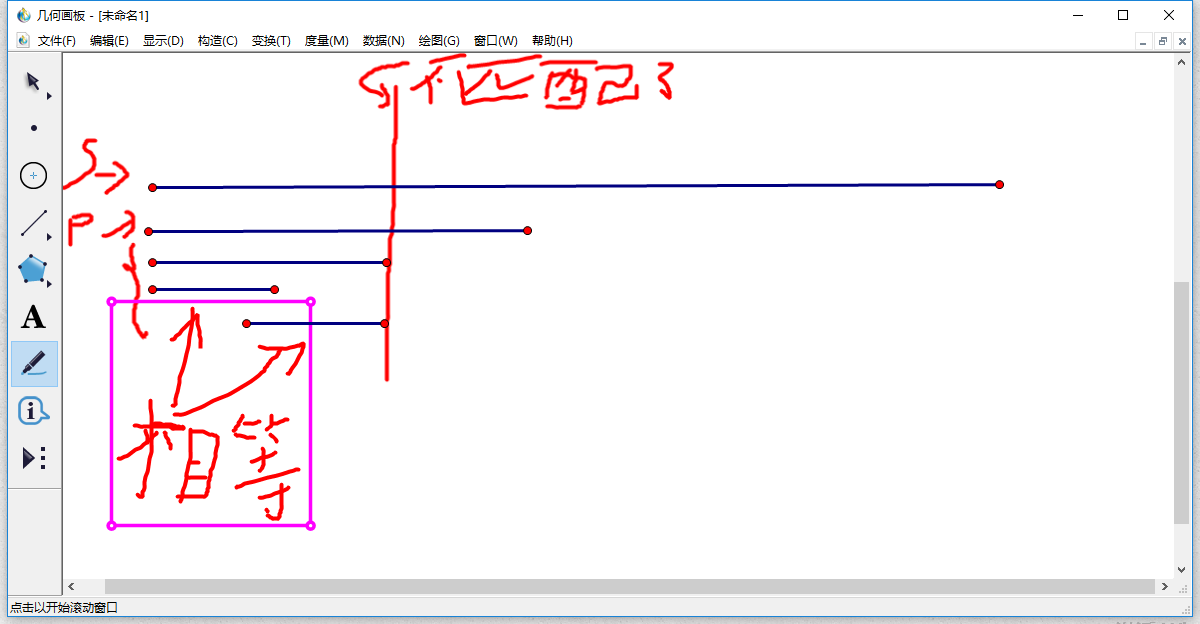
最后两个线段就是表示那个不匹配点的前一个点的前缀和后缀相等，直接从不匹配的这个点的前一个点的next数组再开始遍历就好，不需要去从头开始遍历，这样就可以达到O(n)的复杂度。仔细理解前缀和后缀相等的含义。先假设i为前缀的终点位置用数组表示就是p[1,i]==p[ 不匹配点的前一个点的位置 -i+1,不匹配点的前一个点的位置]，next数组的含义就是这个。

代码（出自yxc大佬）

void kmp()
{
	//next数组预处理 
	for(int i=2,j=0;i<=n;i++)
	{
		while(j&&p[i]!=p[j+1])
		j=ne[j];
		if(p[i]==p[j+1])
		j++;
		ne[i]=j;
	}
	//KMP匹配过程 
	for(int i=1,j=0;i<=m;i++)
	{
		while(j&&s[i]!=p[j+1])
		j=ne[j];
		if(s[i]==p[j+1])
		j++;
		if(j==n)
		{
			cout<<i<<endl;
			j=ne[j];
		}
	}
}