题面描述
Farmer John最近新建立了一个农场,并且正在接受奶牛的畜栏分配请求,有些 畜栏会看到农场美妙的风景。:)
农场由N (1 <= N <= 100,000) 个畜栏组成,编号为1..N,畜栏i可以最多容纳C_i只奶牛 (1 <= C_i <= 100,000)。奶牛i希望得到连续的一段畜栏,表示为一段区间 (A_i,B_i) 。 这样的话奶牛可以在这段牛棚里面转悠。(当然,这段畜栏必须要有足够的空间)
给出M (1 <= M <= 100,000) 个请求,请求出不超过畜栏承载量的情况下,最多可以满足的请求数。
考虑下面展示的一个农场:
编号 1 2 3 4 5
容量 | 1 | 3 | 2 | 1 | 3 |
奶牛1 (1, 3)
奶牛2 (2, 5)
奶牛3 (2, 3)
奶牛4 (4, 5)
FJ 不能够同时满足4头奶牛的请求,否则3,4号畜栏就会有太多的奶牛。
考虑到奶牛2的请求需要一个区间包含3号和4号畜栏,我们尝试这样一种方案,让1,3,4号奶牛 的请求都得到满足,这样没有畜栏超出容量的限制,因此,对于上述情况的答案就是3,三头奶牛 (1,3,4号)的要求可以得到满足。
输入格式
- 第1行:两个用空格隔开的整数:N和M
- 第2行到N+1行:第i+1行表示一个整数C_i
- 第N+2到N+M+1行: 第i+N+1行表示2个整数 A_i和B_i
输出格式
- 第一行: 一个整数表示最多能够被满足的要求数
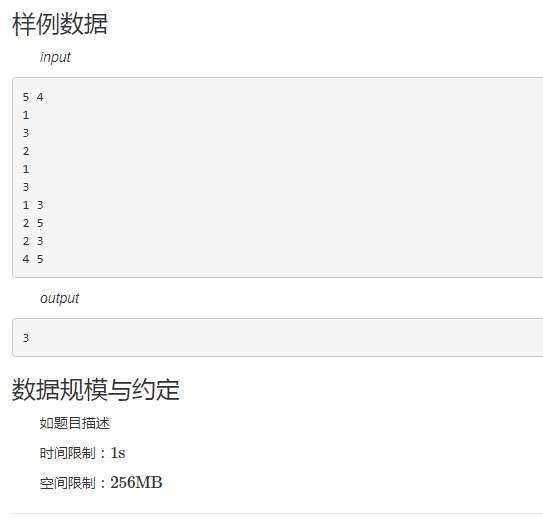
样例
这个题读完题以后我们是可以发现这个很像游荡的奶牛和穿墙人这两个题,一个是不能有交集,一个是不能有超过k个交集,这个是每个点都不一样,那我们还是可以用贪心的思路来搞,先以右节点来从小到大排序,然后用一个线段树来维护,每来一头牛,就把区间减减,到最后查询时>0就是可以,ans++,然后在线段树维护一下最小值,一直保证取最小就好了,这个题我早上写了两小时+,一直在差错误,到最后是因为if语句后多加了个分号,要气死我了,拒绝手抖QAQ
代码
#include<bits/stdc++.h>
using namespace std;
const int oi=1000010;
struct hf
{
int l;
int r;
int dat;
int lazy;
#define dat(x) t[x].dat
#define lazy(x) t[x].lazy
}t[oi*4];
int a[oi];
int n,m;
struct hf1
{
int x;
int y;
}op[oi*4];
bool cmp(hf1 o,hf1 p)
{
return o.y<p.y;
}
void build(int p,int l,int r)
{
t[p].l=l;
t[p].r=r;
if(l==r)
{
dat(p)=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
dat(p)=min(dat(p*2),dat(p*2+1));
}
void spread(int p)
{
dat(p*2)+=lazy(p);
dat(p*2+1)+=lazy(p);
lazy(p*2)+=lazy(p);
lazy(p*2+1)+=lazy(p);
lazy(p)=0;
}
void change(int p,int l,int r)
{
if(t[p].l==l&&t[p].r==r)
{
dat(p)--;
lazy(p)--;
return;
}
if(lazy(p))
spread(p);
int mid=(t[p].l+t[p].r)/2;
if(r<=mid)
change(p*2,l,r);
else if(l>mid)
change(p*2+1,l,r);
else
{
change(p*2,l,mid);
change(p*2+1,mid+1,r);
}
dat(p)=min(dat(p*2),dat(p*2+1));
}
int ask(int p,int l,int r)
{
if(t[p].l==l&&t[p].r==r)
{
return dat(p);
}
if(lazy(p))
spread(p);
int mid=(t[p].l+t[p].r)/2;
if(r<=mid)
return ask(p*2,l,r);
else if(l>mid)
return ask(p*2+1,l,r);
else
return min(ask(p*2,l,mid),ask(p*2+1,mid+1,r));
}
int main()
{
freopen("balloc.in","r",stdin);
freopen("balloc.out","w",stdout);
int ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=m;i++)
{
cin>>op[i].x>>op[i].y;
}
sort(op+1,op+1+m,cmp);
build(1,1,n);
for(int i=1;i<=m;i++)
{
if(ask(1,op[i].x,op[i].y))
{
change(1,op[i].x,op[i].y);
ans++;
}
}
cout<<ans;
return 0;
}