线段树模板

先随便说一下啥是线段树；

字面意思，就是树由线段构成，根节点是1……n，根节点的左儿子是1……mid，右儿子是mid+1……n，以此类推到叶子节点是[i，i]。

下面先来个区间表示的图示

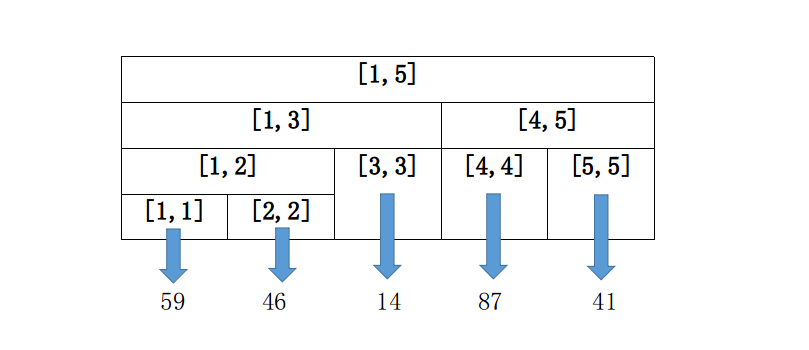
然后就是二叉树形图示

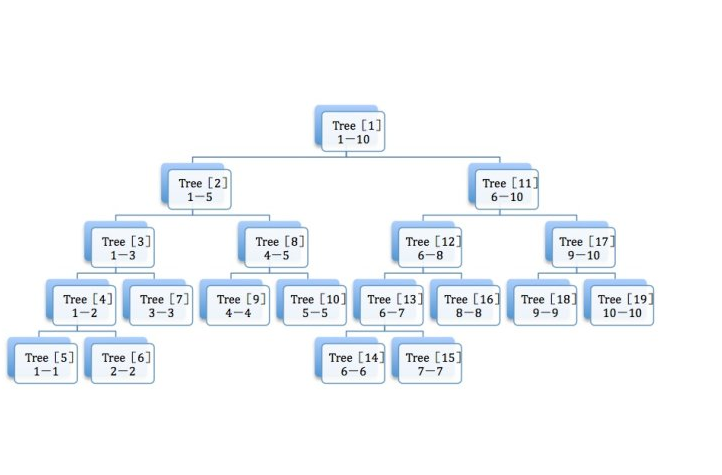
从图上我们可以很清晰的看出二叉树的构造，然后就是各种操作了，建树，单点查询，单点修改，区间查询，区间修改……

首先先说一下建树

建树的话要开4倍空间，因为二叉树的特性是左儿子是根节点的2倍，右儿子是根节点的2倍+1，我们可以根据这个特性来建树，但是会浪费空间，但是这是我们可以接受的，毕竟线段树毕竟高效。

struct hf
{
	int l;
	int r;
	int dat;
	int lazy;
	#define dat(x) t[x].dat
	#define lazy(x) t[x].lazy
}t[oi*4];
void build(int p,int l,int r)
{
	t[p].l=l;
	t[p].r=r;
	if(l==r)
	{
		dat(p)=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	dat(p)=min(dat(p*2),dat(p*2+1));
}

结构体声明和建树代码

void change(int p,int x,int v)
{
	if(a[p].l==a[p].r)
	{
		a[p].dat=v;
		return;
	}
	int mid=(a[p].l+a[p].r)/2;
	if(x<=mid)
	change(p*2,x,v);
	else
	change(p*2+1,x,v);
	a[p].dat=max(a[p*2].dat,a[p*2+1].dat);
}

单点修改代码

int ask(int p,int l,int r)
{
	if(l<=a[p].l&&r>=a[p].r)
	return a[p].dat;
	int mid=(a[p].l+a[p].r)/2;
	int v=-(1<<30);
	if(l<=mid)
	v=max(v,ask(p*2,l,r));
	if(r>mid)
	v=max(v,ask(p*2+1,l,r));
	return v;
}

区间查询代码

区间修改的话需要加一个懒标记下传

懒标记下传代码

void spread(int p)
{
	if(add(p))
	{
		sum(p*2)+=add(p);
		sum(p*2+1)+=add(p);
		add(p*2)+=add(p);
		add(p*2+1)+=add(p);
		add(p)=0;
	}
}

区间修改代码

void change(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))
	{
		sum(p)++;
		add(p)++;
		return;
	}
	spread(p);
	int mid=(l(p)+r(p))/2;
	if(l<=mid)
		change(p*2,l,r);
	if(r>mid)
		change(p*2+1,l,r);
	sum(p)=max(sum(p*2),sum(p*2+1));
}

懒标记和值同时都要++；