线段树模板题2

题面描述

给定一个包含n个数的序列，初值全为0，现对这个序列有两种操作：

操作1：将第k1 个数 到 第k2 个数加1；

操作2：查询 从第k1个数到第k2个数得最大值。（k1<=k2<=n）

所有的数都 <=100000

输入格式

第一行给定一个整数n，表示有n个操作。

以下接着n行，每行三个整数，表示一个操作。

输出格式

若干行，查询一次，输出一次。

样例

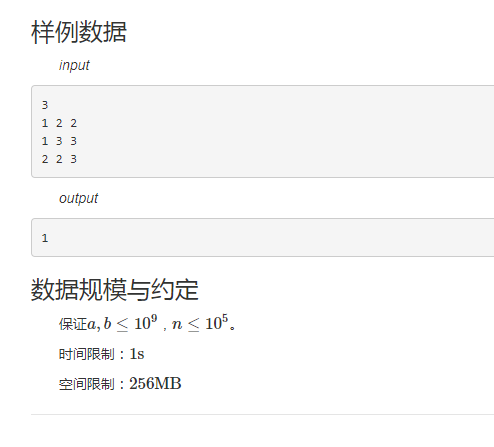
还是线段树的模板题，区间修改，区间查询，需要懒标记

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
struct hf
{
	int l,r;
	int sum,add;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define sum(x) tree[x].sum
	#define add(x) tree[x].add
}tree[100010*4];
int a[100010],n,m;
void b(int p,int l,int r)
{
	l(p)=l,r(p)=r;
	if(l==r)
	{
		sum(p)=a[l];
		return;
	}
	int mid=(l+r)/2;
	b(p*2,l,mid);
	b(p*2+1,mid+1,r);
	sum(p)=max(sum(p*2),sum(p*2+1));
}
void spread(int p)
{
	if(add(p))
	{
		sum(p*2)+=add(p);
		sum(p*2+1)+=add(p);
		add(p*2)+=add(p);
		add(p*2+1)+=add(p);
		add(p)=0;
	}
}
void change(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))
	{
		sum(p)++;
		add(p)++;
		return;
	}
	spread(p);
	int mid=(l(p)+r(p))/2;
	if(l<=mid)
		change(p*2,l,r);
	if(r>mid)
		change(p*2+1,l,r);
	sum(p)=max(sum(p*2),sum(p*2+1));
}
int ask(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))
		return sum(p);
	spread(p);
	int mid=(l(p)+r(p))/2;
	int v=-(1<<30);
	if(l<=mid)
		v=max(v,ask(p*2,l,r));
	if(r>mid)
		v=max(v,ask(p*2+1,l,r));
	return v;
}
int main()
{
	freopen("b.in","r",stdin);
	freopen("b.out","w",stdout);
	cin>>m;
	b(1,1,m);
	while(m--)
	{
		int x,y,z;
		cin>>x>>y>>z;
		if(x==1)
		{
			change(1,y,z);
		}
		if(x==2)
		{
			cout<<ask(1,y,z)<<endl;
		}
	}
}
/*
6 2
1 2 999 4 5 6
C 4 6
Q 4 6
*/