Interval GCD

题面描述

给定一个长度为N的数列A，以及M条指令 (N≤5*10^5, M<=10^5)，每条指令可能是以下两种之一： “C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。 “Q l r”，表示询问 A[l],A[l+1],…,A[r] 的最大公约数(GCD)。

输入格式

第一行两个整数N,M，第二行N个整数Ai，接下来M行每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

样例

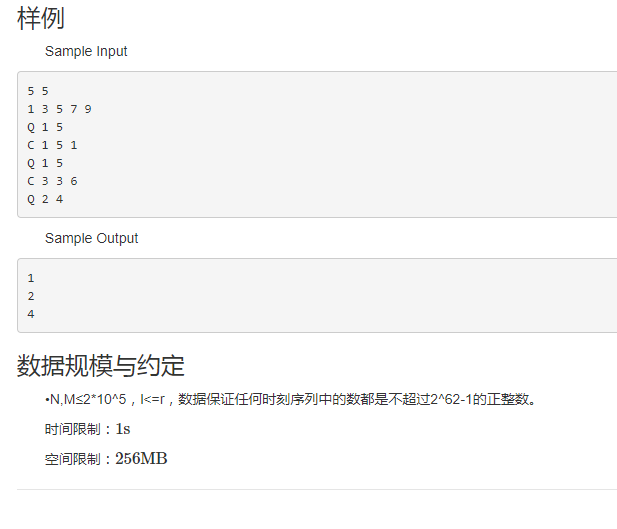
一看这个数据范围我们就可以得知一件事情，一定要用longlong，细节一定要注意，这个题还是比较鬼畜的，还是比较难想的，但是我们可以想到可以对序列进行一个差分的操作，然后可以单点修改就可以成为区间修改，因为差分序列的前缀和是原序列，直接在差分序列上的x+d，y+1的地方-d，最后前缀和序列就是x……y加了d，我们可以用树状数组维护一下。b[i]=a[i]-a[i-1];这样到最后Q l r就相当于是gcd(a[l],ask(1,l+1,r));然后就可以上去搞了，一顿瞎搞即可

代码

#include<bits/stdc++.h>
using namespace std;
struct hf
{
	long long l,r;
	long long dat;
}t[4000010];
long long a[2010000],c[2010000],b[2010000],n,m;
long long gcd(long long q,long long p)
{
	if(p==0)
	return q;
	return gcd(p,q%p);
}
void build(long long p,long long l,long long r)
{
	t[p].l=l,t[p].r=r;
	if(l==r)
	{
		t[p].dat=a[l];
		return ;
	}
	long long mid=(l+r)/2;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	t[p].dat=gcd(t[p*2].dat,t[p*2+1].dat);
}
void change(long long p,long long x,long long v)
{
	if(t[p].l==t[p].r)
	{
		t[p].dat+=v;
		return;
	}
	long long mid=(t[p].l+t[p].r)/2;
	if(x<=mid)
	change(p*2,x,v);
	else
	change(p*2+1,x,v);
	t[p].dat=gcd(t[p*2].dat,t[p*2+1].dat);
}
long long ask(long long p,long long l,long long r)
{
	if(t[p].l>=l&&t[p].r<=r)
	{
		return abs(t[p].dat);
	}
	long long v=0;
	long long mid=(t[p].l+t[p].r)/2;
	if(l<=mid)
	v=gcd(v,ask(p*2,l,r));
	if(r>mid)
	v=gcd(v,ask(p*2+1,l,r));
	return abs(v);
}
void add(long long x,long long d)
{
	for(;x<=n;x+=x&-x)
	b[x]+=d;
}
long long find(long long x)
{
	long long ans=0;
	for(;x;x-=x&-x)
	ans+=b[x];
	return ans;
}
int main()
{
	freopen("test.in","r",stdin);
  freopen("test.out","w",stdout);
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++)
	scanf("%lld",&c[i]);
	for(int i=1;i<=n;i++)
	a[i]=c[i]-c[i-1];
	build(1,1,n);
	for(int j=1;j<=m;j++)
	{
		char op[2];
		long long x,y,z;
		scanf("%s",op );
		scanf("%lld%lld",&x,&y);
		if(op[0]=='Q')
		{
			//cout<<c[x]<<' '<<find(x)<<' '<<ask(1,x+1,y)<<endl;
			printf("%lld\n",gcd(c[x]+find(x),ask(1,x+1,y)));
		}
		else
		{
			scanf("%lld",&z);
			add(x,z);
			change(1,x,z);
			add(y+1,-z);
			change(1,y+1,-z);
		}
	}
 }