分块例题2

题面描述

给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的元素个数。

输入格式

第一行输入一个数字 n

第二行输入 n 个数字，第 i 个数字为a[i]，以空格隔开

接下来输入 n 行询问，每行输入四个数字 opt, l，r，c, 以空格隔开

若 opt = 0，表示将 [l,r] 的之间的数都加 c

若 opt = 1，表示询问[l,r]中 小于c平方 的数的个数

输出格式

对于每次询问，输出一行一个数字表示答案

样例

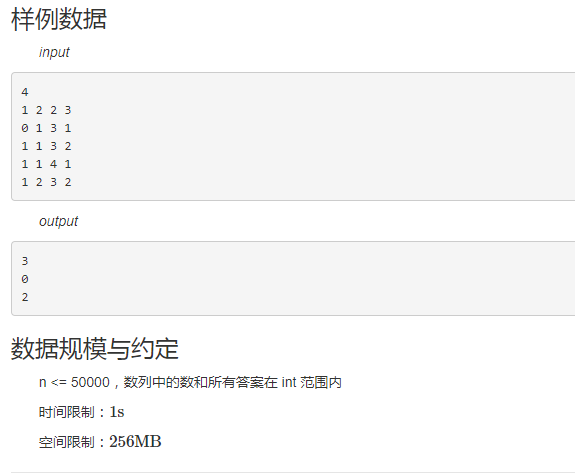
这个题的话用线段树和树状数组就比较困难了，因为是分块例题，那就分块来搞，这个跟上一题差不多，只不过这次是要去维护一个比c平方小的个数 ，就是在改值得时候，用一个vector记录一下这个区间的所有数，排序，在查询的时候先把暴力的解决了，然后在看区间的，因为区间的排过序了，所以直接lower_bound一下，直接答案加上距离他最小的一位数的位置就好了。百行代码甚是恐怖QAQ

代码

#include<bits/stdc++.h>
using namespace std;
int pos[510010],a[510010],l1[510010],r1[510010],add[510010],t;
vector<int >p[510010];
void qing(int x)
{
	p[x].clear();
	for(int i=l1[x];i<=r1[x];i++)
	p[x].push_back(a[i]);
	sort(p[x].begin(),p[x].end());
}
void ch(int l,int r,int d)
{
	//cout<<a[1]<<"                  "<<endl;
	int p1=pos[l],q=pos[r];
	if(p1==q)
	{
		for(int i=l;i<=r;i++)
		{a[i]+=d;
		//cout<<a[i]<<endl;
		}
		qing(p1);
	}
	else
	{
		for(int i=p1+1;i<=q-1;i++)
		add[i]+=d;
		for(int i=l;i<=r1[p1];i++)
		{
			a[i]+=d;
		//cout<<a[i]<<endl;
		}
		qing(p1);
		//a[i]+=d;
		for(int i=l1[q];i<=r;i++)
		{
			a[i]+=d;
		//cout<<a[i]<<endl;
		}
		qing(q);
	//	a[i]+=d;
	}
 } 
 int ask(int l,int r,int c)
 {
 	int p1=pos[l],q=pos[r];
 	int ans=0;
	if(p1==q)
	{
		for(int i=l;i<=r;i++)
		{
			if(a[i]+add[p1]<c)
			ans++;
		//cout<<a[i]<<endl;
		}
		
	}
	else
	{
		
		for(int i=l;i<=r1[p1];i++)
		{
			if(a[i]+add[p1]<c)
			ans++;
		//cout<<a[i]<<endl;
		}
		
		//a[i]+=d;
		for(int i=l1[q];i<=r;i++)
		{
			if(a[i]+add[q]<c)
			ans++;
		//cout<<a[i]<<endl;
		}
		
		for(int i=p1+1;i<=q-1;i++)
		ans+=lower_bound(p[i].begin(),p[i].end(),c-add[i])-p[i].begin();
	//	a[i]+=d;
	}
	return ans;
 }
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	t=sqrt(n);
	for(int i=1;i<=t;i++)
	{
		l1[i]=(i-1)*sqrt(n)+1;
		r1[i]=i*sqrt(n);
	}
	if(r1[t]<n)
	{
		t++;
		l1[t]=r1[t-1]+1;
		r1[t]=n;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=l1[i];j<=r1[i];j++)
		{
			pos[j]=i;
		 } 
	}
	for(int i=1;i<=t;i++)
		qing(i);
	for(int i=1;i<=n;i++)
	{
		int opt,l,r,c;
		cin>>opt>>l>>r>>c;
		if(opt==0)
		ch(l,r,c);
		if(opt==1)
		{
//			for(int i=1;i<=n;i++)
//			cout<<a[i]<<' ';
//			cout<<endl;
			cout<<ask(l,r,c*c)<<endl;
		}
	}
}