分块例题5

题面描述

给出一个长为n的数列，以及n个操作，操作涉及区间开方，区间求和。

输入格式

第一行输入一个数字 n

第二行输入 n 个数字，第 i 个数字为a[i]，以空格隔开

接下来输入 n 行询问，每行输入四个数字 opt, l，r，c, 以空格隔开

若 opt = 0，表示将 [l,r] 的之间的数都 开方

若 opt = 1，表示询问[l,r]中 所有数累加值

输出格式

对于每次询问，输出一行一个数字表示答案

样例

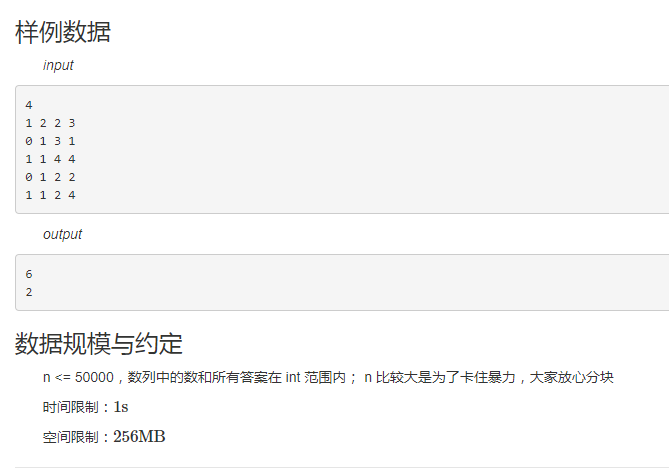
区间开方的话，我们需要知道区间里的所有数，然后去挨个进行开方，这个没法同时做，那分块不就没有用了？相当于暴力？如果没有优化的话确实相当于暴力，但是我们换个思路去想，开方有什么性质？我们是不是可以发现，开方开到最后是不是都是0或1？仔细思考这一点，从这一点入手可以怎么去优化？1开方过后还是1,0不能被开方，那根据这一个性质，我们是不是可以加一个判断，如果这个区间全部都是0或1了，是不是就不用遍历了？仔细思考这一点。那么这样就可以优化许多了，从数据范围分析，每个数不会开方超过四次，所以复杂度是ok的。

代码

#include<bits/stdc++.h>
using namespace std;
long long r[100010],l[100010],sum[100010],a[100010],add[100010],n,t,pos[100010];
bool b[100010];
void change(long long x,long long y)
{
	for(long long i=1;i<=t;i++)
	{
		if(x>r[i]||y<l[i])
		continue;
		if(x<=l[i]&&y>=r[i])
		{
			if(!b[i])
			{
				b[i]=1;
				sum[i]=0;
				for(int j=l[i];j<=r[i];j++)
				{
					a[j]=sqrt(a[j]);
					sum[i]+=a[j];
					if(a[j]>1)
					{
						b[i]=0;
					}
				}
			}
		}
		else
		{
			for(long long j=max(x,l[i]);j<=min(r[i],y);j++)
			{
				sum[i]-=a[j];
				a[j]=sqrt(a[j]);
				sum[i]+=a[j];
			}
		}
	}
}
long long ask(long long x,long long y)
{
	long long ans=0;
	for(int i=1;i<=t;i++)
	{
		if(x>r[i]||y<l[i])
		continue;
		if(x<=l[i]&&y>=r[i])
		{
			ans+=sum[i];
		}
		else
		{
			for(long long j=max(x,l[i]);j<=min(r[i],y);j++)
			{
				ans+=a[j];
			}
		}
	}
	return ans;
}
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	t=sqrt(n);
	for(int i=1;i<=t;i++)
	{
		l[i]=(i-1)*sqrt(n)+1;
		r[i]=i*sqrt(n);
	}
	if(r[t]<n)
	{
		t++;
		l[t]=r[t-1]+1;
		r[t]=n;
	}
	for(int i=1;i<=t;i++)
	{
		for(int j=l[i];j<=r[i];j++)
		{
			pos[j]=i;
			sum[i]+=a[j];
		}
	}
	for(int i=1;i<=n;i++)
	{
		long long op,x,y,z;
		cin>>op>>x>>y>>z;
		if(op==0)
		{
			change(x,y);
		}
		else
		{
			cout<<ask(x,y)<<endl;
		}
	}
}