线段树区间和模板

今日，dxh大佬写了一道区间和的模板题，我发现我并没有写这个模板，于是就去干他一手，n分钟写完了代码，然后查错，查错，就是找不到QAQ，于是又写一遍，结果发现，上一个竟然是少打了=l，我当时就想把电脑砸掉（不要在意）QAQ。

题面描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入格式

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式

输出包含若干行整数，即为所有操作2的结果。

样例

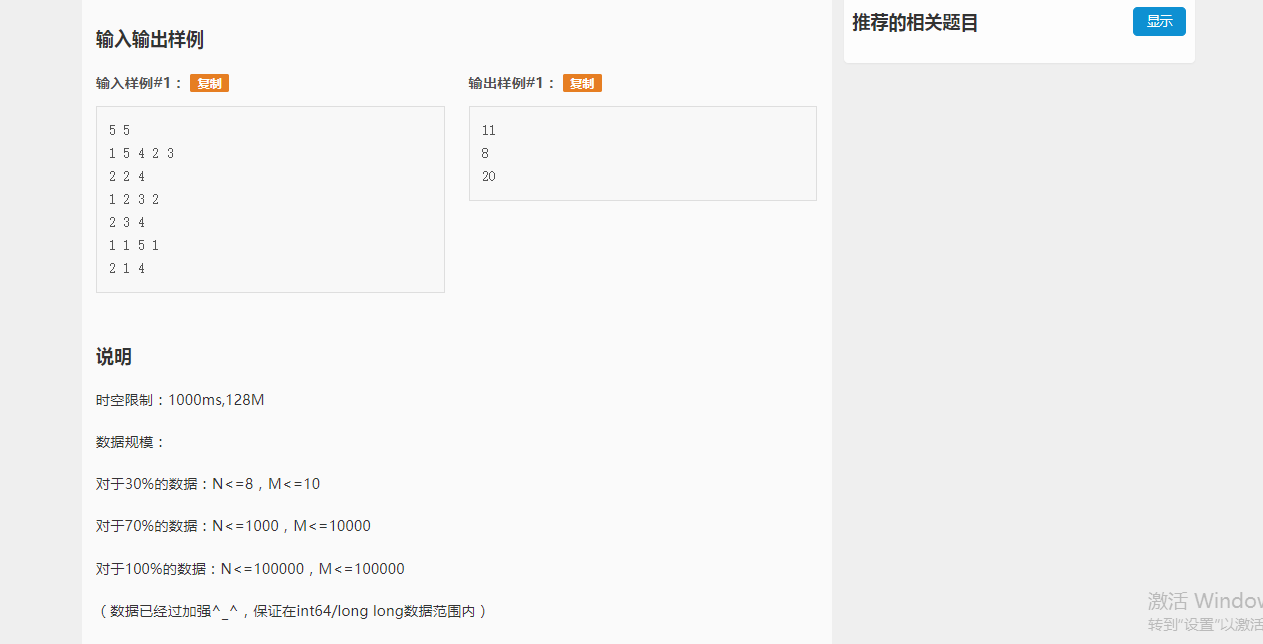
没错，这就是神圣的洛谷题，模板一不先出单点修改，竟然先出区间修改，不知怎么想的，咱也不知道，咱也不敢问QAQ

人性洛谷附解释

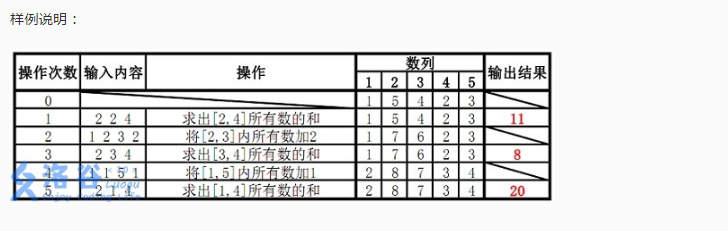
这个就是加一个懒标记，往下传即可，从上往下进行标记，传递信息，写一个pushdown函数进行更新节点信息即可，剩下的就是建树，更改，查询，日常操作QAQ

代码

#include<bits/stdc++.h>
using namespace std;
const int oi=100010;
long long a[oi],n,m;
struct hf
{
	long long l;
	long long r;
	long long dat;
	long long add;
	#define add(x) t[x].add
}t[oi<<2];
void build(long long p,long long l,long long r)
{
	t[p].l=l,t[p].r=r;
	if(l==r)
	{
		t[p].dat=a[l];
		return;
	}
	long long mid=(l+r)/2;
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	t[p].dat=t[p*2].dat+t[p*2+1].dat;
}
void pushdown(long long p)
{
	if(add(p))
	{
		t[p*2].dat+=add(p)*(t[p*2].r-t[p*2].l+1);
		t[p*2+1].dat+=add(p)*(t[p*2+1].r-t[p*2+1].l+1);
		add(p*2)+=add(p);
		add(p*2+1)+=add(p);
		add(p)=0;
	}
}
void change(long long p,long long l,long long r,long long z)
{
	if(l<=t[p].l&&r>=t[p].r)
	{
		t[p].dat+=z*(t[p].r-t[p].l+1);
		add(p)+=z;
		return;
	}
	pushdown(p);
	long long mid=(t[p].l+t[p].r)/2;
	if(l<=mid)
	change(p*2,l,r,z);
	if(r>mid)
	change(p*2+1,l,r,z);
	t[p].dat=t[p*2].dat+t[p*2+1].dat;
}
long long ask(long long p,long long l,long long r)
{
	if(l<=t[p].l&&r>=t[p].r)
	{
		return t[p].dat;
	}
	pushdown(p);
	long long mid=(t[p].l+t[p].r)/2;
	long long sum=0;
	if(l<=mid)
	sum+=ask(p*2,l,r);
	if(r>mid)
	sum+=ask(p*2+1,l,r);
	return sum;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	build(1,1,n);
	for(int i=1;i<=m;i++)
	{
		long long op,x,y,z;
		cin>>op>>x>>y;
		if(op==1)
		{
			cin>>z;
			change(1,x,y,z);
		}
		if(op==2)
		{
			cout<<ask(1,x,y)<<endl;
		}
	}
}