分块例题7

题面描述

给出一个长为n的数列，以及n个操作，操作涉及区间乘法，区间加法，单点询问。

输入格式

第一行输入一个数字 n

第二行输入 n 个数字，第 i 个数字为a[i]，以空格隔开

接下来输入 n 行询问，每行输入四个数字 opt, l，r，c, 以空格隔开

若 opt = 0，表示将 [l,r] 的之间的数都加 c

若 opt = 1，表示将 [l,r] 的之间的数都乘 c

若 opt = 2，表示询问 第 r个数字的值

输出格式

树 对于每次询问，输出一行一个数字对 10007取余的结果 表示答案

样例

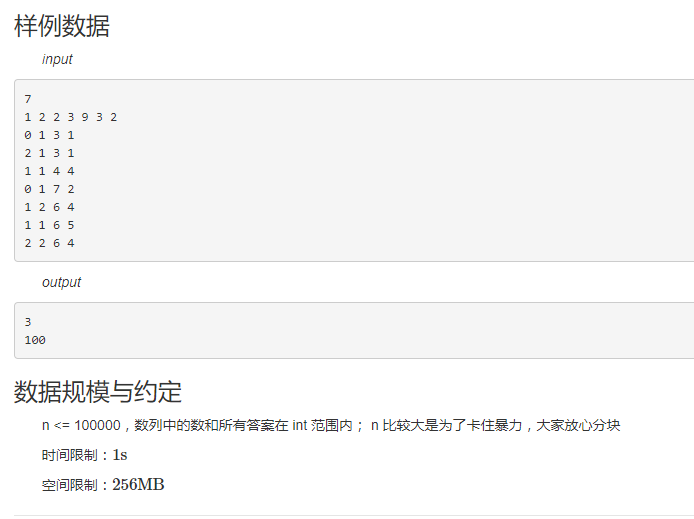
此文章属于补锅，此题已经写了好久了QAQ~这个题大致一看，wow，这不是跟1一样嘛，于是高高兴兴的去写了，但是在写完以后，是错的，仔细一想，乘法的优先级是高于加法的，于是又陷入了迷茫当中。那我们可以在做乘法的时候把加法标记也乘上去，引用hzw大佬的话：

若当前的一个块乘以m1后加上a1，这时进行一个乘m2的操作，则原来的标记变成m1*m2，a1*m2

若当前的一个块乘以m1后加上a1，这时进行一个加a2的操作，则原来的标记变成m1，a1+a2

我们可以这样去处理乘法与加法的优先级问题。

代码

#include<bits/stdc++.h>
using namespace std;
const int oi=10007;
int r[200010],l[200010],ch[200010],a[200010],ji[200010],n,t,pos[200010];
void kl(int x)
{
	for(int i=l[x];i<=r[x];i++)
	{
		a[i]=(a[i]*ch[x]+ji[x])%oi;
	}
	ch[x]=1;
	ji[x]=0;
}
void cheng(int x,int y,int z)
{
	int p=pos[x],q=pos[y];
	if(p==q)
	{
		kl(p);
	}
	else
	{
		kl(p);
		kl(q);
	}
	for(int i=1;i<=t;i++)
	{
		if(y<l[i]||x>r[i])
		continue;
		if(x<=l[i]&&y>=r[i])
		{
			ch[i]=ch[i]*z%oi;
			ji[i]=ji[i]*z%oi;
		}
		else
		for(int j=max(x,l[i]);j<=min(y,r[i]);j++)
		{
			a[j]=a[j]*z%oi;
		}
	}
}
void jia(int x,int y,int z)
{
	int p=pos[x],q=pos[y];
	if(p==q)
	{
		kl(p);
	}
	else
	{
		kl(p);
		kl(q);
	}
	for(int i=1;i<=t;i++)
	{
		if(y<l[i]||x>r[i])
		continue;
		if(x<=l[i]&&y>=r[i])
		{
			ji[i]=(ji[i]+z)%oi;
		}
		else
		for(int j=max(x,l[i]);j<=min(y,r[i]);j++)
		{
			a[j]=(a[j]+z)%oi;
		}
	}
}
int ask(int x)
{
	return a[x]*ch[pos[x]]+ji[pos[x]];
}
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	t=sqrt(n);
	for(int i=1;i<=t;i++)
	{
		l[i]=(i-1)*sqrt(n)+1;
		r[i]=i*sqrt(n);
	}
	if(r[t]<n)
	{
		t++;
		l[t]=r[t-1]+1;
		r[t]=n;
	}
	for(int i=1;i<=t;i++)
	{
		for(int j=l[i];j<=r[i];j++)
		{
			pos[j]=i;
		}
		ch[i]=1;
	}
	for(int i=1;i<=n;i++)
	{
		int op,x,y,z;
		cin>>op>>x>>y>>z;
		if(op==0)
		{
			jia(x,y,z);
		}
		if(op==1)
		{
			cheng(x,y,z);
		}
		if(op==2)
		{
			cout<<ask(y)%oi<<endl;
		}
	}
}