题面描述
人品是必不可少的,人品还是守恒的。每个人的人品都是不同的,并且有正的(选择题可以用骰子全过),也有负的。
海亮高级中学有n (1 <= n <= 100,000)个学生,第i个人的人品值是A_i(-10,000 <= A_i <= 10,000).
海亮高级中学决定重新规划寝室,要让每个寝室的人品和不小于0.寝室的人品和是这个寝室里所有人的人品和。
因为名单是按照学籍号给出的,所以,现在你不能调整学生的顺序,只能按照输入的顺序把学生依次分进各个寝室,当然,为了增加难度,每个寝室的人数可以不同,我们甚至可以把n个学生放在同一个寝室。我们的口号,人品比宿舍重要。
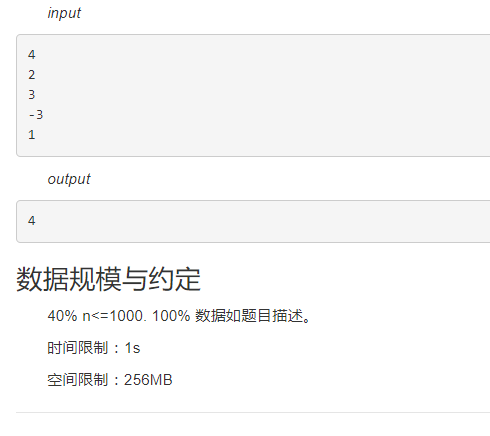
比如现在有4个人,人品分别是2, 3, -3, 1。我们可以按照下面分寝室:
(2 3 -3 1)
(2 3 -3) (1)
(2) (3 -3 1)
(2) (3 -3) (1)
这样保证每个寝室的人品和不小于0.
现在的问题是,如果按照这种原则,有多少种分寝室的方法。当然,方法可能很多,你只需要输出方案数对 1,000,000,009 取余数即可。
输入格式
第一行一个整数n
接下来n行,表示每个学生的人品A_i.
输出格式
一个整数,如题所求的那个余数
样例
emmmmmm,我已经咕了好多天的博客了QAQ,有许多题还没写博客QAQ,回来再慢慢的补吧!现在先写一下这个人品为0的人品题QAQ,此题先想一下裸的DP,要求所有区间是否满足分配原则,可以DP一下,求一个前缀和,相减判断如果满足就加上满足的那个区间的方案数+1,DP方程f[i]+=f[j],当然前提条件是sum[i]-sum[j]>=0,记住,分配原则是不是负数,一定要加等号,然后你就很轻松的写了出来
代码
#include<bits/stdc++.h>
using namespace std;
int sum[100010],f[100010];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
sum[i]=sum[i-1]+x;
}
f[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<i;j++)
{
if(sum[i]>=sum[j])
f[i]+=f[j];
}
}
cout<<f[n];
}
然后你会兴奋的去提交,然后你会发现,TLE,非常舒服,你没有看数据范围,我们可以发现数据范围是十分的大的QAQ,所以,我们可以用树状数组去维护
代码
#include<bits/stdc++.h>
using namespace std;
struct hf
{
long long x;
long long id,kl;
}a[1000010];
long long n,c[1000010];
long long l[1000010],r[1000010];
long long ans=0;
bool cmp(hf o,hf p)
{
return o.x<p.x;
}
inline void add(long long x,long long y)
{
for(;x<=n;x+=x&-x)
{
c[x]=(c[x]+y)%1000000009;
}
return;
}
inline long long ask(long long x)
{
long long res=0;
for(;x;x-=x&-x)
{
res=(res+c[x])%1000000009;
}
return res;
}
int main()
{
freopen("protest..in","r",stdin);
freopen("protest..out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
long long x;
cin>>x;
a[i].x=a[i-1].x+x;
a[i].id=i;
}
sort(a,a+1+n,cmp);
long long pl=1;
for(int i=0;i<=n;i++)
{
a[a[i].id].kl=pl;
if(a[i+1].x!=a[i].x)
{
pl++;
}
}
add(a[0].kl,1);
for(int i=1;i<=n;i++)
{
ans=ask(a[i].kl);
add(a[i].kl,ans);
}
cout<<ans%1000000009;
}
